Factorial ANOVA

In the same way as DV ~ IV is R formula for linear regression or one way ANOVA, the formula for two-way ANOVA is DV ~ IV₁ * IV2 or DV ~ IV₁ + IV₂ + IV₁ : IV₂

Especially the latter one illustrates that we're looking at two predictors and the interaction between those.

Now, we'll apply it to ToothGrowth dataset provided in R.

First, load it:

> attach(ToothGrowth)

Look at the dataset:

> head(ToothGrowth)

Dose is treated as numerical variable, instead we want it to be categorical, let's code the factors

> ToothGrowth$dose = factor(ToothGrowth$dose, levels=c(0.5,1.0,2.0), labels=c("low","med","high"))

See what changed:

> head(ToothGrowth)

Start with some descriptive statistics:

> boxplot(len ~ supp * dose, data=ToothGrowth,

+ ylab="Tooth Length", main="Boxplots of Tooth Growth Data")

You might also check histograms of each factor combination to decide if the mean is an appropriate summary statistic. If this looks okay a useful way to summarise the overall pattern of two-way data is an interaction plot:

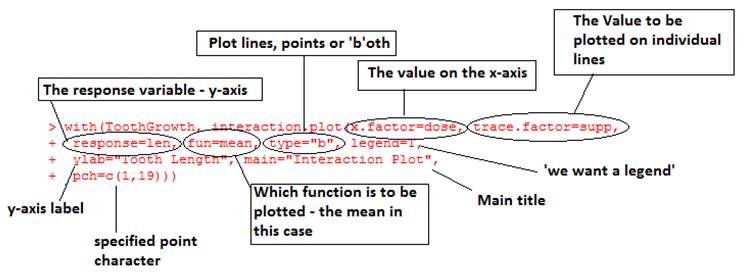
> interaction.plot(x.factor=dose, trace.factor=supp, response=len, fun=mean, type=”b”)

And test the assumption that variances are equal:

> bartlett.test(len ~ supp * dose, data=ToothGrowth)

Now, let's look at the model and the summary:

> model=lm(len~supp*dose)

> summary(model)

also, look at summary.lm() output to see all coefficients.

Same as for one way ANOVA we can also call aov() function:

> aov.out = aov(len ~ supp * dose, data=ToothGrowth)
 
> summary(aov.out)

This allows us to look at the results of planned contrasts:
 
> summary.lm(aov.out)
 
Note that the interaction is significant so we should be careful about interpreting the main effects. We can run post-hoc analysis between all 3*2=6 conditions:
 
> TukeyHSD(aov.out)
 
Or we can restrict it to one predictor (dose):
 
> TukeyHSD(aov.out, which=c("dose"))
 
 

We can test for the effect without the interaction:

> model2=lm(len~supp+dose)

Or could do with interaction but without one main effect

> model3=lm(len~supp+supp:dose)

And could compare whether one model explains significantly more than the other:

> anova(model,model2)

In fact the ANOVA test between models assumes that the simpler model is a strict subset of the other. Is that true in this case?