An Example Program

In this section we develop an example $\alpha$Prolog program which demonstrates how to encode a simple language with names, binding, and capture-avoiding substitution.

For our first example, consider the typed $\lambda$-calculus (a notation for anonymous function definitions). Its syntax is summarized by the following grammar

$$e ::= x \mid e_1 e_2\mid \lambda x.e$$

$$\tau ::= \alpha \mid \tau \to \tau$$

where expression variables $x$ and type variables $\alpha$ are drawn from disjoint, countably infinite sets. We can encode the syntax of $\lambda$-terms using declarations

id  : name_type.
exp : type.

var : id -> exp.
app : (exp,exp) -> exp.
lam : id\exp -> exp.

tid   : name_type.
ty    : type.

tvar  : tid -> type.
arrow : (ty,ty) -> ty.

Here, $id$ and $tid$ are declared to be name types, tnat is, types containing a countable number of distinct names. As in Prolog identifiers starting with an upper-case letter are considered to be variables; undefined lower-case identifiers are considered to be names. The types $exp$ and $ty$ are plain (data)types. We can describe the inhabitants of datatypes (but not name types) via further declarations of constants and function symbols. In this case, there are three function symbols for expressions: variables, applications, and lambdas, and two for types: type variables and function types. The type $id\backslash exp$ that is used as the domain of $lam$ is called an abstraction type, and it denotes the set of expressions with one identifier abstracted. These declarations describe how well-formed terms can be constructed: for example, $lam (x\backslash var (x))$ is an encoding of the identity function and $arrow(tvar(a),tvar(a))$ is an encoding of a type for the identity function.

Since identifiers, expressions, and types are just terms, $\alpha$Prolog can be used to define interesting functions and relations among such terms. These definitions tend to be significantly closer to their ``paper'' presentations than is usual for either functional or logic languages. For example, the following rules express the syntax and typability relation for simply-typed $\lambda$-terms:

$$\infer{\Gamma\triangleright x\!:\!A}{x\!:\!A\in\Gamma} \qquad\inf... ...riangleright \lambda x.M\!:\!A\to B} {\{x:A\}\cup\Gamma\triangleright M\!:\!B}$$

The equivalent $\alpha$Prolog program encoding these rules is

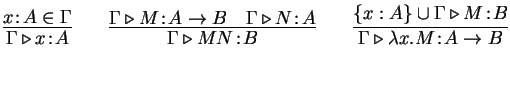
pred of([(id,ty)],exp,ty)
of(Gamma,var(X),A)            :- mem((X,A),Gamma).
of(Gamma,app(M,N),B)          :- of(Gamma,M,arrow(A,B)),
                                 of(Gamma,N,A).
of(Gamma,lam(x\M),arrow(A,B)) :- x # Gamma, 
                                 of([(x,A)|Gamma],M,B).

The first line declares the argument types for the predicate $of$: the first argument is a list of identifier-type pairs representing a context, the second is an expression, and the third a type. The remaining lines are clauses that define the behavior of this predicate. As can be seen, each clause is almost a literal translation of the corresponding inference rule, with $x:A \in \Gamma$ written as mem((X,A),Gamma), $\Gamma\triangleright M\!:\!A$ written as of(Gamma,M,A), and $x \notin FV(\Gamma)$ written x # Gamma.

In Prolog, we might instead encode a binding $\lambda x.e[x]$ as a term $\lambda($``x''$,e[$``x''$)$, that is, using strings or some other data for variables. In $\alpha$Prolog, we think of $\lambda$ as a term constructor mapping abstraction terms $x\backslash e$ to $\lambda x.e$. This view of the world is somewhat similar to that adopted in higher-order abstract syntax, where $\lambda$ is (somewhat circularly) defined as a constructor with type $(exp \to exp) \to exp$. But although there are similarities (for example, both function variables and abstracted names admit equality up to $\alpha$-equivalence), the abstraction type is quite distinct from the function type: for example, there is no built-in application of abstractions, and names are ground terms that can escape the scope of abstractions in limited ways (as does "x" in the last clause of "of").

Another interesting relation (or function) on $\lambda$-terms is substitution. For example, $(x (\lambda y.y))[x/z] = z (\lambda y.y)$. In the $\lambda$-calculus, we ask that substitution not essentially change the ``meaning'' of a term (as a function). To illustrate this point, consider the following flawed definiton of substitution:

$$x[e/x] = e$$

$$y[e/x] = y \qquad (x \neq y)$$

$$(e_1 e_2)[e/x] = e_1[e/x] e_2[e/x]$$

$$(\lambda y.e_1)[e/x] = \lambda y.e_1[e/x]$$

Under this definition, substituting $z$ for $x$ in the term $\lambda x. z+x$ could result in $\lambda x. x+x$, which is a different function. This can be seen by $\alpha$-renaming $\lambda x. z+x$ to $\lambda y.z+y$, in which substituting $x$ for $z$ results in $\lambda y.x + y$. The reason is that in the obvious approach to substitution, variables can be ``captured'' when substitution passes under a binding (as $x$ is when we pass under the $\lambda x$ binder).

The classical approach to this problem is to assume that bound variables are always ``renamed away'' from the all free variables (this is called Barendregt's variable convention). Subject to this convention, the above naive definition becomes correct: equivalently, we can write the fourth clause as

$$(\lambda y.e_1)[e/x] = \lambda y.e_1[e/x]\qquad(y \notin FV(e)\cup\{x\})$$

However, this is not precise enough for a Prolog program to implement, because the implicit, highly nondeterministic ``renaming away'' step needs to be made explicit. Renaming itself also needs to avoid variable capture, so for a mechanical implementation of substitution it is necessary to write down explicitly how to rename/substitute without capture. A typical definition of ``capture-avoiding'' substitution uses a rule

$$(\lambda y.e_1)[e/x] = \lambda z.e_1[z/y][e/x]\qquad(z \notin FV(e)\cup\{x\})$$

This definition renames aggressively, picking a fresh variable $z$ whenever a $\lambda$ binding is encountered.

However, there are problems with turning this definition into a Prolog-style declarative program. For example, the choice of $z$ is very open-ended, and to choose fresh variables $z$ efficiently it is necessary to maintain a ``store'' of unused variable names. This store is passed as an extra argument and return value of $subst$. Also, this definition causes multiple passes to be made over the term because of the renaming. To reduce this to a single pass, we would have to add an additional argument mapping renamed variables to their renamings.

In $\alpha$Prolog, on the other hand, we are able to write a definition that is essentially the same as the declarative definition, yet correct:

func subst(exp,exp,id) = exp.
subst(var(x),E,x)     = E.
subst(var(y),E,x)     = var(y) :- y # x.
subst(app(E1,E2),E,x) = app(subst(E1,E,x),subst(E2,E,x)).
subst(lam(y\E1),E,x)  = lam(y\subst(E1,E,x)) :- y # E, y # x.

where we read $y \mathrel\char93 x$ as $y \neq z$ and $y \mathrel\char93 (E,x)$ as $y \notin FV(E)\cup(x)$. In fact, in $\alpha$Prolog, syntactically distinct name identifiers like $x,y$ are assumed to denote distinct names, so the $y \mathrel\char93 x$ constraints are redundant. On the other hand, we cannot assume that bound variables always are distinct from other variables in scope, so we must check $y \mathrel\char93 E$ in the fourth clause. Because unification in $\alpha$Prolog is up to $\alpha$-equivalence, the implicit renaming step from the declarative definition remains implicit.