Solutions – Practical 4
The code you had to write for this practical gives examples of the basic paradigms for recursion over trees. Unfortunately, the instructions given don’t quite lead to a complete implementation of the optimisations I had in mind.
In this note, I give two “solutions”: one, Optimise, based on the instructions; and another, GoodOptimise, that ignores the erroneous instruction.
reshape
This code gives a template for top-down application of transformations to a tree. The first two lines apply the transformations repeatedly, as long as they apply; the next two lines apply the transformations recursively to subtrees, and recombine the results appropriately; the final line gives a terminal case, it applies only when the recursion reaches a leaf node of the tree.
amalgam
This function again follows the top-down paradigm.
In Optimise, the first six lines apply the transformations repeatedly. (In the first two lines there is no point in reapplying the transformations, as we can see that they would not apply.) The final three lines again implement a top-down recursion over the tree.
The error in the instructions appears here. Consider the expression (5 × 4) + 3 The function amalgam will not reduce this, whereas we would expect it to reduce to the literal, 60. One analysis of the problem is that the transformations
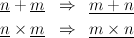
should be applied bottom-up. In GoodOptimise, these transformations are incorporated in the function elim, (by adding them to the subsiduary function delim, since this already uses a bottom-up recursion.
elim
To implement a bottom-up recursion, we separate a single application of a transformation into a subsiduary function, delim, the main function, elim, applies these transformations bottom-up, by first transforming any subtrees, and then attempting to apply a transformation to the result.
rightHeight
This is a straight-forward recursion over the tree; it follows the pattern of the datatype declaration — except that we don’t need to distinguish the two kinds of leaf.
reorder
We apply the re-ordering transformation bottom-up. The subsiduary function order implements the transformation, and the declaration of reorder implements the bottom-up recursion.
optimise
Combining these functions together gives a function that may significantly reduce the size, and stack requirements, of the the stack code produced for an algebraic expression. Other optimisations, such as grouping terms involving the same identifiers, could be included in the same way.
Conclusion
As well as giving examples of top-down and bottom-up recursion over trees, this example demonstrates the subtlety needed to design correct algorithms. The code given by following the original instructions would correctly reduce expressions containing either only additions, or only mutiplications; but it does not cater for the interactions between them.
©Michael Fourman 1994-2006