CS201 Mid-term Examination
University of Western Australia
CS201 Mid-term Examination
Ross Lecture Theatre
Thursday 14th April, 1994
12.00 – 1.00pm
Information
- Regulations governing University Examinations will apply.
- The examination will last 60 minutes, including five minutes reading time.
- Please deposit all books and bags at the front of the lecture theatre.
- Ensure that you are seated by 11.55am.
Instructions
- Your answers should be written, legibly, in the answer-booklet provided.
- This paper consists of four pages, printed on two sides of a single sheet of paper. It contains one short question, A, and three longer questions, 1, 2, 3.
- Your mark will consist of your score on the short question (worth 5 marks), and your best two scores for the three longer questions, (each worth 10 marks).
- You should therefore attempt the short question, and two of the longer questions.
- Short Question 5
marks
Give the responses of the ML system to the following sequence of declarations-
val a = 1;
val b = 2;
val c = 3;
fun f a = let val b = a + c in a + b end;
val b = 5;
f b;
______________________________________________________________________
- Long Question 10
marks
The following datatype can be used to represent trees whose nodes can have an arbitrary number of children.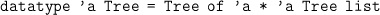
- What tree does the following expression denote (draw a picture):
![Tree(1, [Tree(2, [ ]), Tree(3, [Tree(4,[ ])]),Tree(5,[ ])])](E11x.png)
- Define a function to calculate the number of nodes in such a tree.
- We assign a level to each node in a tree as follows. The node at
the root is at level 1. Its children are at level 2. Their children are
at level 3 and so on.
Define a function countLevel : int -> ’a Tree -> int that counts the number of nodes at a given level of a tree. The expression, countLevel n t, should return the number of nodes at level n in the tree t.
_______________________________________________________________________________________________________________
- What tree does the following expression denote (draw a picture):
- Long Question 10
marks
The EQueue signature is like the signature Queue, but is extended with an additional operation multiple enqueue, menq:(Item list * Queue) -> Queue, intended to add a number of items to the queue in a single operation. The intention is that the items enqueued by a single menq operation may be dequeued in any order, but they must all be dequeued after any items entered in the queue by an earlier enq or menq operation, and before any items entered by any later operation.-
signature EQueue =
sig
type Item
type Queue
val empty : Queue
val enq : (Item * Queue) -> Queue
val deq : Queue -> (Item * Queue)
val menq: (Item list * Queue) -> Queue
end
An implementation of a queue, including this operation, uses the type declaration
-
type Queue = (Item list list) * (Item list list)
the operations empty and menq are implemented as follows:
-
val empty = ([],[])
fun menq(items, (enter, leave)) = (items :: enter, leave)
- Complete the following declarations of the functions enq and deq for
this implementation
-
fun enq(item, ([],leave)) =
| enq(item, ((h :: t),leave)) =
fun deq(enter, (h :: t) :: r) =
| deq(enter, [] :: r ) =
| deq(h :: t, [] ) =
| deq([], [] ) =
- What is the complexity of the three operations
for this implementation?
_______________________________________________________________________________________________________________
- Long Question 10
marks
The PQueue signature is like the signature Queue, but is extended with an additional operation merge:(Queue * Queue) -> Queue, intended to merge together two queues.-
signature PQueue =
sig
type Item
type Queue
val empty : Queue
val enq : (Item * Queue) -> Queue
val deq : Queue -> (Item * Queue)
val merge: (Queue * Queue) -> Queue
end
An implementation of a priority queue of integer priorities represents the queue by a list kept in order of decreasing priority:
-
type Item = int
type Queue = Item list
Here is the function deq: Queue -> int * Queue from this implementation
-
fun deq [] = raise Deq
| deq (h :: t) = (h, t)
- Give an implementation of the operation enq : (int*Queue) -> Queue, compatible with this representation
- Give an O(n) implementation of the operation merge: Queue * Queue -> Queue, compatible with this representation.
- Consider an alternative representation for a priority queue, using an
unordered list to represent the queue. For this representation, the
enq operation is simple
-
fun enq (e, q) = e :: q
Complete the following table giving the complexity of the operations for each representation. (You are not asked to implement all the operations.)
ordered unordered enq O(1) deq O(1) merge
_______________________________________________________________________________________________________________
The End ©Michael Fourman 1994-2006