Sample Exam
1 Introduction
This document contains information concerning the conduct of the mid-term examination, and some sample questions, representative of those that will be set.
2 Information
The mid-term examination for this course will be held, as advertised, on Thursday, April 14th, during the normal lecture period.
- The examination will be held in the normal lecture venue, Ross lecture theatre.
- The examination will last 60 minutes, including five minutes reading time; it will start at 12.00 prompt, and finish at 1.00pm.
- Please deposit all books and bags at the front of the lecture theatre.
- Ensure that you are seated by 11.55am.
3 Sample Questions
The examination will contain one short question (worth 5 marks), and three longer questions. You should attempt the short question, and only two of the three longer questions, each of which will be worth 10 marks.
- 5
marks
Give the responses of the ML system to the following sequence of declarations-
val a = 1;
val b = 2;
fun f a = a + b;
val b = 3;
f b;
- Long Question 10
marks
The following datatype can be used to represent trees whose nodes can have an arbitrary number of children.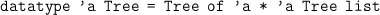
- What tree does the following expression denote (i.e draw a
picture):
![Tree(1, [Tree(2, [ ]), Tree(3, [Tree(4,[ ])])])](L101x.png)
- Define a function to calculate the number of leaves in such a tree.
- We can assign a level to each node in a tree as follows. The node
at the root is at level 1. Its children are at level 2. Their children
are at level 3 and so on.
Suppose we are interested in trees where an internal node at level n always has exactly n children. Define a function check : ’a Tree ->bool that checks whether a given tree has this property.
- What tree does the following expression denote (i.e draw a
picture):
- Long Question 10
marks
The EQueue signature is like the signature Queue, but is extended with an additional operation multiple enqueue, menq:(Item list * Queue) -> Queue, intended to add a number of items (in an arbitrary order) to the queue in a single operation.-
signature EQueue =
sig
type Item
type Queue
val empty : Queue
val enq : (Item * Queue) -> Queue
val deq : Queue -> (Item * Queue)
val menq: (Item list * Queue) -> Queue
end
An implementation of a stack, including this operation, uses the type declaration
-
type Queue = Item list list
the operations empty and menq are implemented as follows:
-
val empty = []
fun menq(items, q) = items :: q
- Complete the following declarations of the functions enq and deq for
this implementation
-
fun enq(item, []) =
| enq(item, (h :: t)) =
fun deq((h :: t) :: r) =
| deq([] :: r) =
| deq [] =
- What is the complexity of the three operations
for this implementation?
- Long Question 10
marks
An implementation of sets of integers is designed to represent a set by a list without repetitions, kept in increasing order. Here is the function union : Set*Set -> Set from this implementation-
fun union(a, []) = a
| union([], b) = b
| union(ah :: at, bh :: bt) =
if ah < bh then ah :: union(at, bh :: bt)
else if ah = bh then ah :: union(at, bt)
else bh :: union(ah :: at, bt)
©Michael Fourman 1994-2006