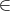 todo, then adj(x) ⊂ todo∪visited.,
todo, then adj(x) ⊂ todo∪visited.,
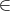 todo∪visited,
todo∪visited,
So far, we have encountered concrete data structures, such as lists and trees. SML makes it particularly easy to use these; they have a natural representation as ML datatypes. Trees allow us to represent a particular class of relationships between data items (lists are a special case of trees). In this note, we introduce graphs. A graph, or network, is a general mathematical structure that can be used to represent many different kinds of relationship between data items. Graph algorithms have numerous applications, both within Computer Science, and in other application areas. There are several different datastructures used to represent graphs; different representations are suited to different purposes. We begin this note with a brief introduction to graphs, and then go on to consider some of these datastructures.
A graph G is a pair (V,E), where V is a set of vertices (sometimes called nodes) and E is a set of edges (sometimes called arcs). Each edge in E joins a pair of vertices from V ; both members of the pair may be the same vertex. Graphs are often viewed pictorially, with circles to represent vertices, and lines connecting circles to represent edges. If the graph is undirected, each edge joins an unordered pair,, {u,v}, of vertices. If the graph is directed, each edge joins an ordered pair, (u,v), of vertices with u called the start vertex of the edge and v called the end vertex of the edge. In pictures, a directed edge is represented by an arrow pointing from the start vertex to the end, u -→ v. If there is an edge joining u to v, we say v is adjacent to u.
In addition to this basic structure, graphs may have information, such as labels or weights, associated with their vertices and/or edges. In pictures, this information can be written beside the arcs and vertices.
A simple example of a graph is an airline route map: here the nodes correspond to airports, and arcs to flights between airports. Some airlines’ route maps may be represented by undirected graphs, however, most airlines have some flights that operate in only one direction, so a directed graph is needed to represent the route information. The nodes of our graph might be labelled with the names of the airports, and the arcs with the distances, or flight numbers.
A quite different example of a directed graph is given by considering a number of interdependent tasks. We can represent the dependencies by a graph, whose nodes are the tasks, with an arc a -→ b representing the fact that task a must be completed before task b is begun. Such graphs arise in project planning and scheduling problems, and also in computer science, where they may be used to represent the dependencies between a number of interdependent computations.
Once you start to look for them, graphs arise naturally in many areas. The unpaved roads of Australia may be represented as a weighted, undirected graph, by taking a node for each road junction, and a weighted edge for each road segment connecting two junctions (the cost of paving the track from a to b is the weight of the edge (a,b)).
A path of length n from x to y in a graph is a sequence ui of n + 1 vertices, with u0 = x, and un = y, that are linked together by n edges ei; the edge ei joins ui-1 to ui. (Note that, according to this definition, there is always a path of length 0, linked together by no edges, from an edge to itself.) In a directed graph we require that all edges in a path point in the same direction; from x, towards y.
We are interested in many properties related to paths in graphs. Here are a few examples. Is there a path joining any two edges, is the graph connected? If it is not connected, how many connected components does it have? What is the shortest path from x to y?
A cycle in a directed graph is a loop—a non-trivial path starting and ending at the same node. A graph with no cycles is said to be acyclic. Directed, acyclic, graphs, or DAGs, are important in many applications.
Once we have represented the data for an application as a graph, we still have to code algorithms to answer the questions we want to ask. For an airline route map we might ask for the shortest way of getting from a to z, this is called the shortest path problem.. For a graph of interdependent tasks we may want to find some order in which we can tackle the tasks so as to respect the dependencies; a solution is called a topological sort of the graph. For a graph representing computations, we may ask which computations are needed to produce a particular result. Abstractly, we want to know which nodes are reachable from the given one. For the graph of Australian dirt roads, we can ask which roads we should pave so as to provide a paved link connecting every pair of junctions, at minimum cost. A subgraph consisting of these segments is called a minimum cost spanning tree..
All these problems may be solved by applying general graph algorithms, which can be studied and implemented in the abstract, and find a wide variety of different applications. We will study these and other algorithms in the next few lectures.
We will consider two approaches to representing a graph. In the first, a graph is viewed as a set of vertices, together with a function, adj, from vertices to sets of vertices, giving the set of vertices adjacent to the given vertex. The set of vertices adjacent to a given vertex can be represented by a list; this gives the adjacency list representation of a graph. In the second family of representations, we directly model the mathematical definition: a graph is represented as a pair of sets; a set of vertices, and a set of edges. Traditionally, the set of edges has been represented by a boolean matrix, giving the adjacency matrix representation of the graph.
Some graphs are sparse, they have few edges, others are dense, they have many edges. Typically, the complexity of a graph algorithm will depend on both V , the number of vertices, and E, the number of edges. Different algorithms and representations may be appropriate for sparse and dense graphs. Sparse graphs are efficiently represented by adjacency lists; an adjacency matrix may be more appropriate for a dense graph. The choice of representation should also take account of the way the graph will be used; for a specific algorithm, the key issues to consider are the time required to perform the graph operations required, and the space required to store graphs.
As an example, consider a directed graph with three vertices, numbered 1, 2 and 3, with edges (1, 2), (1, 3) and (3, 2). With the first method, this graph could be represented by:
val g = [(1, [2, 3]),
(2, []), (3, [2]) ]; |
Here, an association list has been used to represent the connection between a vertex and the set of adjacent edges. These sets of edges are represented as lists; the set of vertices is implicit as the set of keys to the association list. This representation implicitly uses the type
type Graph = (int * int list) list
|
We can use an explicit function to represent the association between a vertex and its adjacency list. This gives the following representation of our example graph:
val g = ([1,2,3], fn 1 => [2,3] | 2 => [] | 3 => [2])
|
Which corresponds to the type
type Graph = ((Vertex list) * (Vertex -> Vertex list);
|
The graph could be represented as a pair of sets, as follows:
val g = ([1, 2, 3], [(1,2), (1,3), (3,2)])
|
Here each set is represented by a list. This uses the type
type Graph = ((Vertex list) * ((Vertex * Vertex) list));
|
For yet another variation, we could use a functional representation of one of the sets
val g = ([1,2,3],
fn (1,2) => true | (1,3) => true | (3,2) => true | _ => false) |
type Graph = ((Vertex list) * ((Vertex * Vertex) -> bool));
|
The possibilities are endless. We will use the ML module system to organise the morass. Before introducing a general signature giving a general-purpose interface to graphs, we see how a simple interface, based on the idea of an adjacency-list representation, allows us to describe and investigate a fundamental algorithm for graph search.
We use an interface to provide access to an adjacency-list representation of a graph, while hiding inessential details of the implementation. The essential feature provided by the interface is that, given a graph and a vertex we can produce a list of adjacent vertices.
The functor DFS uses this interface to produce a function reachable, that gives a list of vertices reachable by a path from a given vertex in a graph.
Exercise 1 Write structures, matching the argument signature of DFS, using each of the four representations of graphs, with integer nodes, outlined in the previous section.
The algorithm is based on the idea that the two list parameters to the auxiliary function dfs represent sets of nodes. At any call dfs todo visited of the auxiliary function,
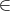 todo, then adj(x) ⊂ todo∪visited.,
todo, then adj(x) ⊂ todo∪visited.,
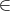 todo∪visited,
todo∪visited,
These properties are valid for the initial call of dfs, and are preserved by each recursive call.
If the function dfs terminates, we can conclude that the value, visited, returned is indeed the set of nodes reachable from s, since on the last call of dfs the list todo is empty. Finally, the number of vertices and edges in a graph is finite; apart from the start node, which is placed in todo for the initial call, a node is added to todo at most once for each edge leading to that node, because when an edge is considered, its start vertex is added to visited. Each non-terminating call of dfs removes a node from todo. This can happen at most E + 1 times, where E is the number of edges in the graph. So the function terminates.
The size of visited is bounded by V , the number of vertices in the graph, so each call to member has cost O(V ). As we have seen, there are at most E + 1 such calls, so the cost of calls to member is O(V × E). Later, we will describe graph representations for which adj has O(lnV ) .
To complete the analysis, we consider the cost of calls to adj and append. There are at most V calls to adj; if the cost of a call to adj is O(E) then calls to member will dominate the total cost.
The call to append, used to add items to todo has a cost proportional to the number of items added. The total cost of these calls is therefore O(E). Adding this to the equation does not alter the complexity.
Depth-first search is an efficient strategy for exploring reachable nodes. We can picture the strategy in terms of an explorer systematically investigating an estuary with many channels and islands. The vertices of the graph are junctions between channels; the channels form the edges. The graph is directed; the arrows point upstream. Beginning at a vertex u, the sea, the explorer goes upeach channel in turn, to visit those vertices v for which there is an edge (u,v). While visiting a vertex that has not been previously visited, the explorer recursively repeats the visiting process. The name ‘depth-first’ arises from the fact that the search always attempts to explore more deeply into the graph, all the way to the source of each tributary, before backtracking to continue visiting other neighbours of a vertex.
The order of exploration is just like the post-fix ordering of a tree. The root of a tree is the start vertex and the leaves are vertices from which no further exploration is possible. Graph search is more involved because we have to keep tack of nodes we have visited to avoid re-visiting old ground. Without keeping track we might even get stuck forever in a cycle. As with tree traversal, there is scope for different ordering of behaviour at vertices: pre-order style, post-order style, and various types of in-order style.
Since the lists used by dfs represent sets, we can modify the DFS algorithm by using different representations for these sets. A different implementation of visited could provide a more efficient membership test, and dramatically change the complexity of the algorithm. A different implementation of todo could alter the order in which we recurse through the nodes of the graph. We can express this in ML using the module system. We replace the list todo by a stucture supporting the queue operations empty, isEmpty, enq, menq, deq; and visited by a structure supporting the set operations, empty, insert, member.
|
The effect of our earlier implementation could be obtained by using a stack as the “todo” queue, and our most simple, list-based, implementation of sets as the “visited” set. As other implementations of the todo queue give different search orders, we have changed the name of the auxiliary function to search. Of itself, this general function doesn’t do much—we simple return the set of reachable nodes as before. However, we can further modify the code to find paths in a graph.
The functor PATHSEARCH produces a function that keeps track of
|
the path by which we arrived at a given node. The function searches for a path between two nodes of a graph. The todo queue contains paths represented as lists of nodes these are initial segments of attempts to find a path from start, s, to finish, f. (Notice how this is shown in the parameter specification for the functor.) At each application of the auxiliary function, a path is removed from the queue. If the queue is empty then there is no path. If the last node in this path (at the head of the list as we build the paths in that order) has already been explored, we discard the path. Otherwise, we check to see if we have reached out goal, (Vertex is declared as an eqtype so we can do this). If so we return the path as result; if not we add every adjacent vertex to form a list of new paths, one step longer, which are placed in the todo queue, we also record the fact that we have visited this node.
Notice that the paths placed in the queue are one step longer than the one we removed. If we implement the queue as a queue, we can argue that we will always consider all shorter paths before any given path. We initialise the queue with a path of length 0. When we remove a path of length n, we may add some paths of length n + 1, but they go at the end of the queue; all paths of length n will be removed before we consider any path of length n + 1. This variant of the algorithm therefore finds a shortest path from start to finish (if there is a path at all).
(C) Michael Fourman 1994-2006