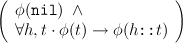 →∀l ⋅ φ(l)
→∀l ⋅ φ(l)
In previous lecture notes we have seen how to carry out inductive proofs on lists and trees. To re-cap, here are the datatype definitions, and the associated inductive proof rules:
datatype ’a list = nil
| :: of ’a * ’a list |
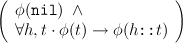 →∀l ⋅ φ(l)
→∀l ⋅ φ(l)
datatype ’a tree = Leaf
| Node of ’a tree * ’a * ’a tree; |
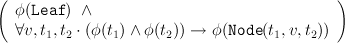 →∀t ⋅ φ(t)
→∀t ⋅ φ(t)You should be able to start noticing a pattern here. In both datatypes we can build larger instances of the structure by applying a constructor to smaller instances (using :: and Node). There are also constructors that act as a base case (nil and Leaf). The format of the associated induction rules mirrors the way these structures are built. Let’s examine the datatype bexp, which represents simple Boolean expressions.
datatype Bexp = V of string
| /\ of Bexp * Bexp | \/ of Bexp * Bexp | ~ of Bexp; |
This datatype has more constructors than trees or lists, but the basic idea is the same. We have some constructors for building expressions out of existing types (in this case V) and some constructors for building expressions out of smaller expressions (in this case /\, \/ and ~). The format of the associated inductive rule shouldn’t be too surprising:
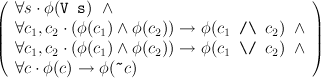 →∀c ⋅ φ(c)
→∀c ⋅ φ(c)You should be able to follow the pattern to produce induction rules for many datatypes of this form. Try to do this for some of the variations of the tree datatype illustrated in earlier notes. This kind of induction is known as structural induction. Most finite datatypes admit this kind of inductive proof technique, although in some cases the form of the inductive rule can be a bit messy. For example, consider a tree datatype where we allow an arbitrary number of children at each node:
datatype ’a tree = Node of ’a * (’a tree list);
|
Can you write down the structural induction rule for this type?
The technique does not work on datatypes built from functional values. For example, consider
datatype funny = F of funny -> funny;
|
We cannot get a structural induction rule for this datatype, and so we cannot use induction to prove that a property φ holds for all objects of type funny. Dealing with datatypes such as this is outside the scope of the course. However, most datatypes do not make use of such functional values, and so this limitation is not particularly serious.
A binary relation ≺ is well-founded if there exist no infinite decreasing chains
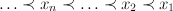
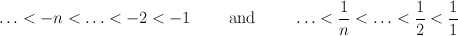
Why all this interest in well-founded relations? Suppose ≺ is a well-founded relation over some type α, and φ(x) a property to be proved for all x of type α. The technique of well-founded induction can be used to prove this. The induction rule may be written as
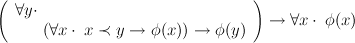
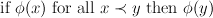
All of the induction rules we have seen up to this point can be obtained from this rule by suitable choice of the well-founded relation. If ≺ is
A well-founded relation given by a measure function yields induction on the size of an object.
Let ≺ be a well-founded relation over some type α. If f is a function with formal parameter x that makes recursive calls f(y) only if y ≺ x, then f(x) terminates for all x. In this case, we say that f is defined by well-founded recursion on ≺. Informally, f(x) terminates because, since there are no infinite decreasing chains in ≺, there can be no infinite recursion.
Proving that a function terminates suggests a useful form of induction for it. If a function is defined by well-founded recursion on ≺, then its properties can often be proved by well-founded induction on ≺.
We have seen how functionals can be used to write very concise programs. We would like to be able to prove some properties of such functionals. For example, if we have two functions, f and g, and we map g over a list l and then map f over the result, then we would expect to get the same result if we map f o g over l, i.e. we would like to prove that
(map f) o (map g) = map (f o g)
|
Before we attempt to prove such an equivalence we need to clarify what we mean by equality here. The law of extensionality states that functions f and g are equal if f(x) = g(x) for all x (of suitable type). The extensionality law is valid in ML because the only operation that can be performed on an ML function is application to an argument. If two functions are extensionally equal, then replacing one by the other doesn’t affect the final result (we are assuming for simplicity that all functions terminate). Some languages (notably LISP) regard two functions as being equal only if their definitions are identical. LISP uses this intensional equality because it views a function value as a piece of code that can be taken apart. If we stick to extensional equality we can prove that (map f) o (map g) is indeed equal to map (f o g). We just have to apply both sides of the equality to an arbitrary list l and then simplify. Now (map f) o (map g) l = map f (map g l) and so we must prove that for all l,
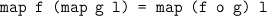
Such equivalences are important to a compiler writer. We might express our algorithm in terms of two separate maps for clarity. This is often the case when the functions (map f) and (map g) perform interesting tasks in their own right. However, it is clearly inefficient to first map g over a list and then to map f over the result. It is better to map f o g over the list in one go. Proving such equivalences allows a compiler writer to transform programs to more efficient ones whilst guaranteeing that the observable behaviour of the program remains unchanged.
(C) Michael Fourman 1994-2006