CS201 mid-term examination(60 minutes)
Answer all four questions.
-
- Give SML definitions of the list functions
map: (’a -> ’b) -> ’a list -> ’b list and
filter: (’a -> bool) -> ’a list -> ’a list. - The function fmap combines the actions of these two functions.
It is defined by
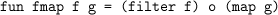
- Prove that the two expressions (map f) o (map g) and map (f o g) are always equivalent if f and g are pure functions, i.e. involving no exceptions or other side-effects.
- Give SML definitions of the list functions
- The following datatype can be used to represent trees where nodes can have
an arbitrary number of children.
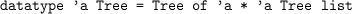
- What tree does the following expression denote (i.e draw a
picture):
![Tree(1, [Tree(2, [ ]), Tree(3, [Tree(4,[ ])])])](midterm2x.png)
- Define a function to calculate the number of leaves in such trees.
- We can assign a level to each node in the tree as follows. The node at the root is at level 1. Its children are at level 2. Their children are at level 3 and so on. Suppose we are interested in trees where a node at level n always has exactly n children if it is not a leaf. Define a function to check whether a given tree has this property.
- What tree does the following expression denote (i.e draw a
picture):
- Give the responses of the ML system to the following sequence of declarations
- The following function for exploring
local fun listall [] acc = acc
| listall (T (a,children) :: trees) acc = listall(children @ trees) (a :: acc)
in
fun dfs t = listall t []
end - Write a function nodes: tree -¿ int -¿ int such that nodes n t gives the number of nodes of depth n in the tree t.
-
fun accsum (Lf a, acc) = a + acc
| accsum (Nd(l,v,r), acc) = accsum(l, accsum(r, v + acc))
fun sumtree (Lf a) = a
| sumtree (Nd(l,v,r)) = sumtree l + v + sumtree rShow, by tree induction, that accsum(t, acc) = sumtree t + acc
- Complexity??
Part 2 (90 minutes)
Answer any two of the following four questions.1
- A priority queue is similar to a normal queue except that each item has a
priority associated with it. When retrieving an element the one with the
highest priority is chosen. If more than one element has this priority then
the one that was inserted first is chosen. We can use the following
signatures to define such queues.
-
signature Q_ELMT =
sig
type T
val priority : T -> int
end
signature PQUEUE =
sig
type T
structure Element: Q_ELMT
val empty: T
val insert: T * Element.T -> T
exception Empty
val remove: T -> (Element.T * T)
end
- Provide an implementation of the functor
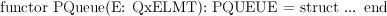
- Use this functor to build a structure for manipulating priority queues of strings, where shorter strings have higher priority than larger ones.
- Use your solution to (b) to implement a sort function on lists of strings.
- Modify your code (and the signatures provided) so that the remove function removes all occurrences of the element at the head of the queue. The result of the call should be the element, the number of times it appeared in the queue, and the queue that results from its removal.