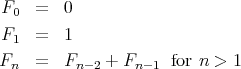
Before starting this practical you should read Lecture Note 1, and the note Using Poly/ML.
This practical is designed to get you familiar with the SML programming environment. You should work through it while interacting with the SML system — in subsequent practicals, you will be expected to spend more time thinking about the problems involved before rushing to the nearest workstation! Don’t worry if you don’t understand all of the following material completely — after all, that’s what the lecture course is for. However, you will get more out of this practical if you think about what you are typing, rather than just entering expressions in a mechanical fashion. Lab demonstrators are around to answer your questions while you are using the SML system, so please feel free to ask questions when you need help.
The final section of the practical contains questions that you should be able to answer by analogy with similar examples provided in the text. They all require you to write some ML code. Your assessment will be based on this code, which should be placed in a file, as described in the Instructions at the end of this note, before 6 pm on Thursday 11th March. You should follow the instructions carefully, as the assessment process will be partially automated, and errors may result in your work being ignored. This practical contributes 4% to your final CS201 mark.
In this practical you will see several types of data value: booleans, strings, integers, and reals, as well as pairs and tuples of values. These are used because they are simple data types that should be familiar, so we can all agree on a starting point. Most of the examples here are concerned with computing mathematical functions. Subsequent practicals will include more complex data types that can be used to model real-life entities, so please don’t let this practical give you the idea that SML is only of use to mathematicians.
For this practical, you start the SML system by typing the command “fep ml prac1” for a stand-alone interactive session, or “ml prac1” if you are running ML from within the emacs editor (see the note Using Poly/ML for details). You should get something similar to the following response:
Poly/ML runtime system version 2.06MX-SUN (10:56 Thu 01 Jul 1993)
Running with heap parameters (h=1024K,ib=204K,ip=90%,mb=204K,mp=50%) . . . > |
The “>” is SML’s prompt, i.e., it is waiting for input at this point. If you want to interrupt the SML system at any time, you should just type Ctrl-C, A new prompt, “=>” will then be displayed. Then type a character: q(uit - Exit from system), c(ontinue running), or f(ail - Raise an exception)
Try typing the following expressions and see what happens:
2 + 3;
2 * 3; 2 + 2 * 3; (2 + 2) * 3; |
The “;” at the end of each expression tells the SML system to go away and evaluate the expression. Note that the system returns not only a result, but also its type.
It quickly becomes tedious to type in such expressions directly to the SML system, particularly when you make a mistake. There are a number of solutions to this problem. You can recall and edit a previous line using fep control keys (e.g., Ctrl-P and Ctrl-N to move backwards and forwards in the history of input lines, and Ctrl-B and Ctrl-F to move within a line). For longer SML inputs, where line-by-line interaction with the SML system is not required, it is more convenient to put everything into a file. You can then cut and paste between editor and SML windows, or you can tell the SML system to read the file using the command “PolyML.use "filename";”. The note Using Poly/ML outlines a number of ways of creating and editing your ML code. A common mistake is to edit a file to fix a bug, but then forget to save the file before instructing SML to read it. The data read will then be that before the bug fix, which is often the source of much confusion.
It’s annoying to keep typing “PolyML.use”. We can give this function a shorter name, say “use”, by typing the following val declaration at the “>” prompt:
val use = PolyML.use;
|
Note the semi-colon, which tells the system to compile the preceding declaration. We can now just type “use "filename";” to read a file. We can also give the string “"filename"” a name
to avoid repeatedly typing quotes. You can then just type use prac1; to read your file.
You can define functions in SML using a fun declaration. Try typing the following into a file, and then load it into SML using use. Note that negative numbers in SML are written using ~, as in ~1, ~3 etc.
fun max (x, y) = if x > y then x else y;
max (2, 2+1); max (max (2, 1), max (~1, ~4)); |
Notice that, when SML compiles a function, it returns the type of the function. In this case, the type is int*int -> int. This means that max takes a pair of integers, int*int, as argument, and returns an integer, int, as result.
Most functions you will write in SML are recursive. For example, the factorial function can be written as:
fun fact 0 = 1
| fact n = n * fact (n-1); |
Try applying fact to some examples, including a large number such as 1000. What happens when you apply fact to a negative number?1 To catch this error we might redefine fact as follows:
fun fact n =
let fun natfact 0 = 1 | natfact n = n * natfact (n-1) in if n < 0 then error "fact called with negative argument" else natfact n end; |
Try applying this function to ~1 and see the difference.
We now investigate the execution speed of various functions. For this practical, a function time has been provided: it takes a function and a list of arguments and applies the function to each argument in turn. The result is a list containing pairs of the argument and the time it took the function to execute on the argument. The execution stops as soon as the execution time exceeds a limit, and so for a slow function only some of the arguments in the list may be used. The units of time are unimportant: we are mainly interested in comparing the execution times on different sizes of argument, rather than looking at the absolute values. Suppose the time to execute fact(n) was t. What would you expect the execution time of fact(2 * n) to be? Try executing the expression:
time fact [64,128,256,512,1024,2048,4096];
|
Does the result confirm what you expected? If not, can you suggest why? [Hint: try evaluating fact 256. Do you think it can be held in a normal size integer register?]
Let’s try some other functions. The Fibonacci numbers may be defined by:
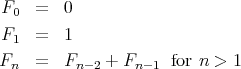
fun fastfib 0 = (0, 1)
| fastfib n = let val (prev, curr) = fastfib (n-1) in (curr, prev + curr) end; |
Evaluate fib and fastfib on some examples to convince yourself that they both compute Fibonacci numbers. Time fastfib to check the claim that it is much more efficient.
Another simple example is to compute the greatest common divisor of two numbers (i.e., the largest integer that exactly divides both numbers) using the relationship:
fun gcd (m, 0) = m
| |
We can time the efficiency of this function, but this time we must provide a list of pairs of integers, as gcd requires a pair of numbers. Try typing:
val x = 12345678;
val l = [(13,x),(14,x),(15,x),(16,x),(17,x),(18,x),(19,x),(20,x)]; time gcd l; |
The result is rather boring as gcd is so fast. Try replacing time by map in the last line, i.e., evaluate map gcd l. Can you guess what map does? Test out this guess by trying some other examples, such as map fact [1,2,3,4,5,6].
For our final example, let’s try raising a number x to a power n. This can be done using repeated multiplication:
fun power (x, 0) = 1
| power (x, n) = x * power(x, n-1); |
Test its performance by executing the following:
fun pair_with m n = (m, n);
pair_with 2 10; val pair_with_two = pair_with 2; pair_with_two 10; val l = map pair_with_two [128,256,512,1024,2048,4096,8192,16384]; time power l; |
A ‘faster’ way of calculating a power exploits the relationship x2k = (x2)k:
fun fastpower (x, 0) = 1
| fastpower (x, n) = if n mod 2 = 0 then fastpower (x*x, n div 2) else x * fastpower (x*x, n div 2); |
(“div” is the SML integer division operator, in C it is called “/”.)
Execute time fastpower l to check that there is an improvement. Now compare power and fastpower for computing large powers of 10. Can you explain why fastpower is less impressive than it was for powers of two? [Note: the explanation is not straightforward.]
So far, our examples have used integers. For this practical arithmetic operations (such as *) have been set up so that, by default, they apply only to integers. To gain access to operations on reals try typing
open Real;
|
This opens a structure called Real, set up expressly for this practical. An ML structure groups together a collection of types, functions and values. You can also try opening two other structures, Integer, and String. The contents of all these three structures are normally available by default in Standard ML. Try some experiments, then restore the environment you will need for the assessed part of the practical by typing
open Integer;
|
Finally, here are some simple problems to test your understanding of this practical.
Define a function FF:int -> int such that FF(n) gives the least number of nodes in such a tree of height n. Declare two integer values FF20 and FF200 giving the answers to the two questions posed.
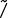 CS201/Prac1, create a file called Answers1.ML
containing the ML code for your answers.
CS201/Prac1, create a file called Answers1.ML
containing the ML code for your answers.
At the beginning of the file 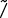 CS201/Prac1/Answers1.ML, before your
code, place the line
CS201/Prac1/Answers1.ML, before your
code, place the line
structure Answers1 : A1 = struct
at the end of the file, after your code, place the line
end;
Finally, for reference, here is the signature of the structure you are asked to create. You don’t need to input this signature as it has been declared in the prac1 database. It provides a summary of the values you should implement.
signature A1 =
sig (* Question 1 *) val C : int*int -> int (* Question 2 *) val FF : int -> int val FF20 : int val FF200 : int (* Question 3 *) val G : int*int -> int (* Question 4 *) val RB : int -> int val RB100 : int end; |