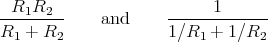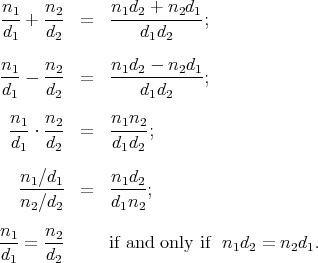
In this practical, you will learn to use products to represent other types of data, and use ML structures and signatures to control the specification and implementation of a new type.
Your work will be assessed on the basis of the correctness of the two structures you implement. Part 1 carries 60% of the marks for this practical; the remaining 40% are allocated to Part 2.
This practical continues the mathematical flavour of the first practical. However, this time, some more interesting data types are involved. The exercises cover two different kinds of useful mathematical object: rational numbers, and approximate real numbers.
Both of these are types of number. For each of them, you asked to provide an implementation matching the signature NumberSig.
To avoid confusion with the existing arithmetic operators, we call the operators ++, --, **, //, , and ==; we make the binary operators infix, and give them the same precedence as their real counterparts.
For this practical, you should use the command ml prac2 to start your ML session. This provides a few general functions1 , including the functions error and time you used in Practical 1, and includes the following infix directives:
Suppose that we want to do arithmetic with rational numbers. That is, we want to be able to add, subtract, multiply and divide them and also to test whether two rational numbers are equal. The following relations define these operations in terms of the numerators and denominators of the rational numbers:
(* rationals -- (numerator, denominator)*)
type num = int * int; |
Your code for this part should be placed in a file CS201/Prac2/Rational.ML The exercise involves doing two things:
Suppose now that we wish to manipulate inexact quantities (such as those measured parameters of physical devices) with known precision so that, when computations are done with these approximate quantities, the results will be numbers of known precision. One approach is to represent a number by an interval that gives the range of possible values of an inexact quantity. Then the result of adding, subtracting, multiplying or dividing two intervals is itself a new interval representing the range of the result. We can represent an interval by a pair of reals:
(* interval of uncertainty (lowerBound, upperBound) *)
type num = real * real; |
To simplify the analysis, we will always assume that the first number is no larger than the second number. (Later in the course, we will see how this convention can be enforced in the SML language through the use of abstract datatypes.)
You should provide an implementation of interval arithmetic Interval:NumberSig. Your code for this part should be placed in a file CS201/Prac2/Interval.ML The exercise involves doing two things: