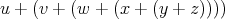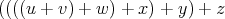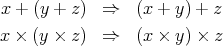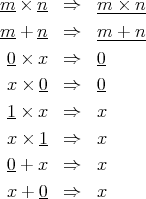Aims

In this practical, you will learn to reshape trees.

Assessment

Your work will be assessed on the basis of the correctness of the functions you implement. Your code should have the structure described in the section Practicalities, and be placed in the file CS201/Prac4/Optimise.ML under your home directory. The assignment of marks to the various components of the exercise is given, as comment, in the signature OptimiseSig. This weighting is not intended to reflect the relative difficulty of implementing the various functions; it is designed to ensure that those who do a reasonable job on the heavily weighted functions get a reasonable mark, while those who seek an excellent mark have to work for it.

Deadline

The revised deadline for this practical is 6.00pm, Friday 15th April.

Introduction

Seldom does a programmer have the luxury of starting from a clean slate. In this practical, you will modify, and improve on, an existing system. Code for this system is given, and documented, in an appendix to this document. However, you don’t need to understand the implementation details of the code provided in order to complete the practical.

In this practical we use syntax trees to represent algebraic expressions. The existing system provides an implementation of the abstract syntax of expressions, and functions to compile, and execute, code to evaluate an expression. It uses a stack-based, evaluator; “compilation” is accomplished by post-fix traversal of the syntax tree.

Optimisation

The stack code produced for an expression may be unneccessarily inefficient. Evaluating the stack code for an expression may require a deeper or shallower stack, depending on the way the expression is written. Expressions involving only constants may be evaluated, once and for all, at ‘compile time; our code generator produces code to evaluate them at run time. Algebraic manipulation of the expression, before compilation, could lead to better code.

Your task is to apply simple algebraic transformations to the syntax tree, before passing it to the compiler, in order to optimise the code produced. You should perform four optimisations, in turn: reshaping, constant amalgamation, constant elimination, re-ordering. These are described individually below.

Before you start coding your solutions, you should make sure you understand what is required. To consolidate your understanding, draw diagrams of the trees involved, for some simple examples.

Four optimisations

reshaping

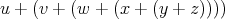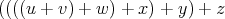Code for the expression produces the RPN code “u v w x y z  +   +   +   +  +”, which stacks up all the arguments before doing any addition. The algebraically equivalent expression produces the stack code “u v + w + x + y + z +”. This only requires a stack of depth 2.

You should write a function reshape: Expn -> Expn to implement this optimisation. Your function should apply one of the left-rotations¹ :

to reshape the tree, wherever possible. It seems easiest to do this top-down; you should apply the rules repeatedly to a tree, and then apply the same rules to the subtrees of the result. To reshape a tree:

• if it matches one of the patterns above, apply the transformation, and then reshape the resulting tree;
• otherwise, if it is a sum or product recursively reshape each of its subtrees;
• otherwise it is a leaf, leave it alone.

constant amalgamation

The expression, ((x + 3) + y) + 7, produces the stack code, “x 3  +  y  +  7 +”. The algebraically equivalent expression, (x + y) + 10, produces the code “x y  +  10 +”.

Our next two optimisations cooperate to combine and eliminate constants. Since constants may be separated in the tree, as in the example just given, we may have to collect them together before performing any arithmetic. Your second optimisation should be a function that collects together and amalgamates constants.

You should write a function amalgam: Expn -> Expn. Your implementation should assume that sequences of additions or multiplications are associated to the left; later you will use the optimisation of the previous section to reshape the tree before applying this function. The following rules² , applied top-down, will amalgamate multiple constants, occurring on the right-hand-side of an operator, in a sequence of multiplications, and push the product down the tree:

Your function should include similar rules for addition.

constant elimination

Once constants have been amalgamated by the function amalgam, we can complete the elimination by evaluating constant expressions. In a few special cases—addition of 0, multiplication by 0 or 1—we can eliminate constants altogether. Here are the revelant algebraic transformations:

You should write a function delim : Expn -> Expn that performs the transformation if any of these apply, and otherwise returns the expression unchanged. Then write a function elim : Expn -> Expn that applies delim bottom-up: given a tree,

• if it is a sum or product, first recursively eliminate constants from each of its subtrees (this may reduce one of the subtrees to a constant), then apply the transformations to the resulting tree;
• otherwise it is a leaf, leave it alone.

re-ordering

The depth of stack required to evaluate the RPN code for a given binary tree is one more than the right-height of the tree; the right-height of a leaf is 0, the right-height of a node is the maximum of,

• the right-height of the left subtree, and
• 1 plus the right-height of the right subtree.

The commutative laws for addition and mutiplication

may be applied, judiciously, to reduce the right-height of a syntax tree. For example, the tree representing a + (b× (c + d)) has right-height 3, while the algebraically equivalent expression, ((c + d) × b) + a has a right-height of 1.

You should write a function rightHeight : Expn -> int to compute the right-height of a syntax tree, and another reorder : Expn -> Expn that applies the transformations given above, bottom-up, whenever the right-height of x is less than the right-height of y. This means that you should recursively apply the transformation to the two subtrees before seeing if you need to adjust a node.

Finally, you should combine your optimisations into a single transformation, using the ML infix operator o for function composition:

val optimise = reorder o elim o amalgam o reshape;

Practicalities

If you run ML with the command ml prac4, the identifiers ++ and ** will be set up as infix, with their usual precedences. But, in order to make it easy to exercise your optimisations, they have been made right-associative. All the structures documented in the appendix are predefined in the prac4 database.

As usual, a signature, OptimiseSig, (see Figure 1) has been given for the code you are asked to write. You should place your code in a structure Optimise:OptimiseSig in a file Prac4/Optimise.ML. Any functions you have been unable to implement should be replaced by dummies of the correct type.

Appendix - stack-based evaluation of expressions

This appendix documents the code provided for the practical. The information provided here goes beyond what you will need to complete the practical, but it should be of general interest.

The code provided has four main components:

• a structure Expn which provides a datatype Expn representing the abstract syntax of expressions.
• A structure, Environment, providing an implementation of the dictionary signature EnvironmentSig given in Figure 2.
• A structure Machine which provides a type Action of stack-machine instructions, and a function, execute, for executing sequences of these instructions,
• a structure Compile which provides a compilation of stack code from abstract syntax, and

These components are used by the structure TopLevel to implement a simple, but fairly powerful, expression evaluator, that will compile a list of declarations.

Abstract syntax of expressions

infixr 6 ** infixr 4 ++  
 
structure Expn = struct  
datatype Expn =  
         Id    of string      (* identifiers    *)  
       | Lit   of int         (* literals       *)  
       | op ++ of Expn * Expn (* addition       *)  
       | op ** of Expn * Expn (* multiplication *)  
end

The abstract syntax provides for algebraic expressions in + and ×, with integer constants, and arbitrary strings as identifiers.

The environment

The values associated with identifiers will be stored in a datatstructure called the environment. The signature EnvironmentSig, see Figure 2, provides an interface to the structure Environment, which uses an association list, a (string*int) list of pairs, each consisting of a string and the associated integer value, as an underlying datastructure. This implementation has, intentionally, been made transparent, in order that you can see the effects of declarations as they are made.

We will use the value empty to represent a new environment, the function enter to add new bindings to an environment, and the function lookup to find the value associated with a given string.

The abstract machine

The structure Machine, given in Figure 3, provides a model for a stack-based evaluator. The machine has four actions: we can push a literal, or the value of an identifier, onto the stack, or apply one of the arithmetic operations, +, and × to the top two elements of the stack.

Code for the evaluator consists of a list of actions. The function run is constructed by specifying the state transition corresponding to the execution of each Action. The components of the state are: args, an argument stack; and code, a list of actions. The environment, needed by the machine to look up the values of identifiers, is passed as a parameter, env.

To execute a given code, we perform each of the actions in turn, starting with an empty stack. Running code compiled from a syntax tree should leave a single value on the stack. This value is returned as the result.

Compilation

infixr 4 ++  
infixr 6 **  
 
structure Compile =  
struct  
local open Expn Machine  
      fun codeacc (Id s,   rest) = PushVal s :: rest  
        | codeacc (Lit n,  rest) = PushLit n :: rest  
        | codeacc (a ++ b, rest) = codeacc(a, codeacc(b, Add :: rest))  
        | codeacc (a ** b, rest) = codeacc(a, codeacc(b, Mul :: rest))  
in  
   fun code expn = codeacc(expn, [])  
end  
end;

The function, code, produces the stack code for a given expression. It is based on the post-order traversal of a binary tree described in the notes.

infixr 4 ++  
infixr 6 **  
 
structure TopLevel =  
struct  
local  
fun adddecs ((s,e) :: decs) env =  
       let val v = Machine.execute env (Compile.code e)  
       in adddecs decs (Environment.enter((s,v), env)) end  
  | adddecs [] env = env  
in  
  fun compile decs = adddecs decs Environment.empty  
end  
end;

The structure TopLevel uses the evaluator to compile and run a sequence of declarations. As an example of its use, consider the following ML code

open Expn TopLevel;  
 
val a = Id "a" and b = Id "b" and c = Id "c"  
 
val mydecs =[ ("a", Lit 4),  
              ("b", a ++ Lit 1),  
              ("c", a ** b),  
              ("a", a ++ c) ];  
 
val finalEnv = compile mydecs;

Running this produces the output

val finalEnv = Env [("a", 24), ("c", 20), ("b", 5)] : Dict

Compare this with the following ML code:

val a = 4;  
val b = a + 1;  
val c = a * b;  
val a = a + c;  
 
(a,b,c);

which produces the final response

> val it = (24, 5, 20) : int * int * int

Concluding remarks: Functions and Environments

Interaction with the ML system generates an environment in which future declarations are evaluated, just like the compile function provided by the structure TopLevel. The similarity goes much deeper; by choosing the oppropriate environment for evaluating the code for an expression, we can implement let expressions and functions. The body of a let expression is evaluated in an environment including the bindings generated by the local declarations, but these are not added to the top-level environment. When we apply a function, the body is evaluated in an environment which binds the formal parameters to the values of the actual parameters. Taking these ideas a litte further would allow us to implement recursive functions, and curried functions. But we are already well away from the substance of the practical.