Stacks and Queues
In previous notes and practicals, we have used products, records and lists to build representations of a variety of different kinds of data: rational numbers, polynomials, sets. We have used signatures to specify interfaces for manipulating various kinds of data, and seen that we can sometimes give a variety of different implementations for the same interface.
Signatures allow us to separate the specification of a package from its implementation. However, our treatment so far has not given such a clear separation of implementation and use. The user of a package can by-pass the interface, and access the implementation directly. In this note we introduce the ML abstype construct, which allows us to prevent this. We will introduce new interfaces, and implementations, for various types of queue. These illustrate the use of abstract types, and will provide a basis for the study of more refined implementations, covered later in the course.
1 The Need for Abstract Data Types
In Lecture Note 6, we described a package for manipulating sets. Sets were represented by lists:
-
type Set = int list
Some of our set operations relied on the “fact” that lists representing sets contain no duplicates; but any list may be passed as a set, and a programmer could all too easily pass a list with duplicates into the system — with unpredictable consequences. We could have used a datatype declaration, such as
-
datatype Set = Set of int list
to make this kind of error less likely. But, it would still be possible (and sometimes tempting) to by-pass the interface and make direct use of the representation. What is wrong with accessing implementations directly? We begin this note by discussing three aspects of this question.
Modularity Later in the course we will introduce other implementations of sets. Suppose we have written a client program that uses the IntSet package, and wish to use a different set package, for example, one implemented using a binary search tree. If the client program manipulated the list representations of sets directly, it would have to be changed to use the new representation of sets. A client program that only manipulated sets using the functions provided in the Set signature would be easier to maintain. The task of writing the program might be slightly harder, as all of the operations you might wish to perform on a set would have to be expressed in terms of the given functions. The temptation to drop down to the underlying representation to implement a function may be quite strong. However, if one can resist this temptation, the resulting program will have the desirable property of being independent of the representation chosen to implement the set package. As long as the same set of functions is provided for each choice of representation then your program should work unchanged.
Of course you might start off with good intentions, but then accidentally exploit your knowledge of the particular representation, a list in this case. It would be good if the system could prevent us from making such mistakes.
Equality Consider the two sets {1, 2, 3} and {3, 2, 1}, as sets, they are identical. So the values, Set [1,2,3] and Set [3,2,1], represent the same set. However, two values of a datatype are equal if they are built using the same constructor and the underlying values are the same. The lists [1,2,3] and [3,2,1] are not equal, and so, as far as our programs are concerned, neither are the two sets! There is a mismatch between the equality we would like to have defined on sets, and the equality provided by the system. This is not the system’s fault — it doesn’t know what a set is. The problem arises whenever a representation allows a number of different data values to represent the same logical value. In our particular example, each permutation of the values in a list represents the same set. One solution would be to introduce another invariant, and always represent our sets by lists in a given order. Then each set would have only one representation. This might be a good solution in this case, as we could exploit the extra invariant to improve the efficiency of our package. However, in other examples it might be costly to maintain such a canonical representation, that is, a choice of particular representation for each value. Another solution is to define an equality function that allows for the possibly different permutations of the elements and to use this function for all our set equality tests. Unfortunately, it is very easy to accidentally write S1 = S2 somewhere in our client code, thus introducing a subtle error. From the client program’s point of view, this ‘equality’ test is non-deterministic; given (two representations of) the same set, as S1 and S2, it sometimes returns true, and sometimes false! Fortunately, ML provides tools to eradicate such aberrations. Non-deterministic code (in other languages) leads to madness, and explains a thriving market in “debuggers” that allow the programmer to examine low-level details of underlying representations, in an effort to understand what their code is doing.
Safety The set package can exploit the fact that each set is represented by a list without duplicates. For example, if we are trying to remove an element e from a set represented by a list s we can stop as soon as we find the first occurrence of e. There can’t be any others. Furthermore, we can prove that every set constructed using the set functions provided by the package is represented by a list with no duplicates, and so this optimisation is sound. Unfortunately, if the user of the set package is allowed to construct sets using the Set constructor explicitly then this “invariant” can break down, as in Set [1,1,1,1]. Let us summarise our discussion:
- Safety
- In some cases the implementer of a package would like to force a programmer using the package to use only a given collection of functions to manipulate a type — rather than allowing him/her direct access to the representation. This allows the implementation to exploit invariants preserved by these functions, that might be destroyed by access to the representation.
- Modularity
- In some cases, we, as programmers, would like the system to check that we are only using a given collection of functions to access a package. If we adhere to this discipline, we can replace one implementation of a package by another, without altering our program. A mechanical check can ensure that we don’t inadvertently break the rules.
- Equality
- A final point is that the notion of equality provided by the system may not agree with notion of equality appropriate for the objects we want to represent. In such cases we would like to hide the system equality function.
2 The abstype Construct
Representing a set directly as a list allows us to treat any list as a set. If, instead, we use a datatype declaration,
-
datatype Set = Set of int list
we introduce a new type. We can use the constructor Set to construct sets from lists and, using pattern-matching, to extract lists from sets. Hiding the constructor from the user would bar this access to the representation. Of course, to implement the operations on sets we need access to the constructor, so we need a means to limit the scope of the constructor. We can do this using signatures and structures. Consider the implementation given in Figure 1.
Since the signature SetSig doesn’t include the constructor Set, the constructor is not visible when we open the structure.
- Preventing access to the constructor Set guarantees that the user cannot create values of type Set that violate our invariants.
- Since Set is a new type, the only operations we can use for manipulating it are those provided by the interface. Unfortunately, there is one exception to this rule:
- Equality on Set, interpreted as equality of the underlying representations, cannot be hidden by restricting the signature. Some implementations may use a canonical representation, others will not. Since the difference is visible to the user, we lose some of the benefits of abstraction.
What we need, is a construct that will limit the scope of constructors, and hide the equality function on representations. The abstype declaration does precisely this. It is like a datatype declaration except that the constructors of the datatype, and the equality test on members of the type, are only in scope within a range of declarations (the declarations that provide the interface to the type). If we want an equality function, it must be implemented explicitly. An implementation of SetSig using an abstract type is given in Figure 2
|
Here, abstype ... with ... end forms a construct analogous to local ... in ... end. The implementation of the type Set, given between abstype and with is only visible as far as the corresponding end. The declarations between with and end are visible outside this block, but the constructor Set, and the equality test on sets, are not. Values of type Set will not be displayed at the top-level, as this would give the game away about the underlying representation. You need to ensure that the functions defined between with and end are rich enough for your purposes. Once you have passed the end the barriers are up! You cannot peek inside the representation later if you realise that one of the functions you need cannot be expressed in terms of the interface. A type whose representation is hidden, is known as an abstract data type (ADT). The ML abstype declaration allows the user to implement secure abstract data types.
You should be able to replace one abstract type by another, based on a different representation, as long as the interface remains the same. The fewer components we have in the interface, the easier it is to change the representation. When we design the interface to an abstract type, there is a delicate balancing act to perform: placing too few functions in the interface may lead to problems expressing an operation in terms of the functions provided; too rich an interface creates a lot of unnecessary work every time you create a new implementation of the type.
3 Examples
We now look at some further examples of abstract data-types. We specify and implement various kinds of queue. A queue is a data-structure used for storing and retrieving data items. Figure 3 gives a signature that will match many different implementations of queues.
|
The name comes from an analogy with queues formed by people waiting for busses, hamburgers, theatre tickets, or what have you. Just as with these examples, our queues allow for arrivals, enqueue, enq, and departures, dequeue, deq; a queue represents a bag1 of items, enqueue adds an item to this bag, dequeue chooses an item to remove from the queue (if it is not empty). Just as with human queues, our queues will vary according to the rule used to choose the next item to remove from the queue. It is traditional to give the basic operations different names, depending on the rule we are using; this can help to avoid confusion. However, using the general signature for different kinds of queue will allow us to make our code more modular, later, when we discuss algorithms based on the different kinds of queue.
We will introduce three different rules:
- FIFO Queue
- First in, first out; this is the rule followed in the well-ordered, ideal, queue in which newcomers stand at the back, and service is from the front. When we talk about a queue without further qualification this is the rule we have in mind; we use the signature QueueSig for these.
- Stack
- Stacks follow a rule that goes to the the other extreme: last in, first out (LIFO) the last arrival is served first. Stacks are widely used in computer science; but are not popular as queues in the real world. The traditional names for the operations on stacks are push, (enqueue), and pop, (dequeue); they are said to derive from the analogy with the spring-loaded stack of plates found in cafeteria. We will use these traditional names, to avoid confusion, when discussing stacks and queues informally, but, not in our code, as this would make it harder to re-use.
- Priority Queue
- Items are ordered by priority. The queue member of highest priority is served first, irrespective of the order of arrivals. This rule requires some structure on the type of items: an ordering, to determine the relative priorities of different items.
We will give implementations of all three kinds of queue, using lists to build our underlying representations. We begin with stacks, because these are the simplest.
Stack An implementation is given in Figure 4, placing items on the stack is implemented by cons, and removing them is implemented by splitting a list into head and tail.
|
This amounts to a renaming, and repackaging of the basic operations on lists. Each of the operations takes O(1) time.
Queue A queue can also be represented using a list, as in Figure 5. The head of the queue is the head of the list. When we add a new item to the queue, we have to do some work to send it to the back; queue insertion takes O(n) time due to the use of append.
|
An alternative representation for queues, given in Figure 6 uses a pair of lists. We remove elements from the front of the second list and insert elements to the front of the first. If the second list is empty, we replace it by the (reversed) contents of the first:
|
The analysis of this implementation of the function deq introduces a new idea. When you remove an element from the queue, it normally takes O(1) time. However, when the “out” list is empty, the cost of a call to deq is clearly O(n) due to the use of rev. There is more to be said: since each element placed on the queue, and later removed, is passed from one list to the other exactly once, the average time for each operation is constant. We say the amortised cost of each operation is O(1).
Priority Queue To implement a priority queue, we keep a list in sorted order, highest priority at the head. This makes the code for deq simple, but means that we need an auxiliary function, insert, to place an item in the correct position in a list when we call enq. Figure 7 gives an implementation of a priority queue containing integers — where larger integers have higher priority.
|
Since insert must traverse the list of items waiting in the queue, the complexity of enq is O(n), where n is the number of items in the queue. Later, we will see much better implementations of priority queues.
4 Types and Abstraction
Abstraction is important in programming as it allows us to manage complexity. In ML, abstraction is provided by hiding information: using signatures, and datatypes, we can hide some aspects of the implementation of a package; the abstype declaration provides an alternative mechanism for hiding information.
Using signatures is a more flexible mechanism. But it does not allow us to hide the equality test on a type. We need to do this when there are multiple concrete representations of a single abstract value. Furthermore, we should do it if there is any possibility that we may want to use such a representation in the future; otherwise, any client code may make use of the equality, and present porting problems when we change our implementation.
Our implementations of stacks and queues of integer could clearly be mimicked for any type of item. Indeed, we could make the Queue type polymorphic; we can code the implementation with no knowledge of the type of item that will be stored in the queue. However, our implementation of priority queues depends on the priority ordering between elements, so we can’t make this type of queue polymorphic. For this reason, we chose a monomorphic Queue type for our signature. Later, in Lecture Note 12, we will introduce ML functors, which will allow us to give a general implementations of queues and stacks, parameterised on a type of item; and an implementation of priority queues, parameterised on a type and a priority ordering.
5 Specification
We have presented signatures as specifications, and so they are. The examples of this note make it clear that a signature on its own is not a sufficient specification; a queue is not acceptable as an implementation of a stack – although the signatures are the same.
A fuller specification of a stack would include properties that the various functions in the interface should satisfy. For example, the equation
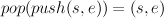
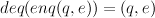
Similarly, a queue implementation should have the property that if q is a non-empty queue, and
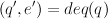
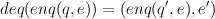
Add here specifications of stacks and queues.
Giving correct, concise, and comprehensible specifications is hard. Showing that a given implementation satisfies the properties specified is sometimes harder. Often, the best we can do is to use straightforward implementations, such as those given in this note, as specifications of the required behaviour. We can then attempt to verify that other, more recondite, implementations are indistinguishable from these prototypes. We will return to these issues later in the course. ©Michael Fourman 1994-2006