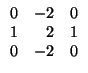B-Rep
b-spline
b-spline fitting
b-spline snake
back projection
back-propagation
back-tracking
background
background labeling
background modeling
background normalization
backlighting
bandpass filter
bar
bar detector
bar-code reading
barrel distortion
barycentrum
bas-relief ambiguity
baseline
basis function representation
Bayes' rule
Bayesian classifier
Bayesian filtering
Bayesian model
Bayesian model learning
Bayesian network
BDRF/BRDF
beam splitter
behavior analysis
behavior learning
Beltrami flow
bending energy
best next view
Bhattacharyya distance
bi-modal histogram
bicubic spline interpolation
bidirectional reflectance distribution function
bilateral filtering
bilateral smoothing
bilinear interpolation
bilinearity
bin-picking
binarization
binary image
binary mathematical morphology
binary moment
binary noise reduction
binary object recognition
binary operation
binary region skeleton
binocular
binocular stereo
binocular tracking
biometrics
bipartite matching
bit map
bit-plane encoding
bitangent
bitshift operator
blanking
blending operator
blob analysis
blob extraction
block coding
blocks world
blooming
Blum's medial axis
blur
border detection
border tracing
bottom-up
boundary
boundary description
boundary detection
boundary grouping
boundary length
boundary matching
boundary property
boundary representation
boundary segmentation
boundary-region fusion
bounding box
BRDF/BDRF
breakpoint detection
breast scan analysis
Brewster's angle
brightness
brightness adjustment
Brodatz texture
building detection
bundle adjustment
burn-in
butterfly filter
B-rep: See surface boundary representation .
b-spline: A curve approximation spline represented as a combination of basis functions:
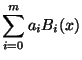
b-spline fitting: Fitting a b-spline to a set of data points. This is useful for noise reduction or for producing a more compact model of the observed curve.
b-spline snake: A snake made from b-splines .
back projection: 1) A form of display where a translucent screen is illuminated from the side not facing the viewer. 2) The computation of a 3D quantity from its 2D projection. For example, a 2D homogeneous point
background: In computer vision, generally used in the context of object recognition. The background is either (1) the area of the scene behind an object or objects of interest or (2) the part of the image whose pixels sample from the background in the scene. As opposed to foreground . See also figure/ground separation .
background labeling: Methods for differentiating objects in the foreground of images or those of interest from those in the background .
background modeling: Segmentation or change detection method where the scene behind the objects of interest is modeled as a fixed or slowly changing background , with possible foreground occlusions . Each pixel is modeled as a distribution which is then used to decide if a given observation belongs to the background or an occluding object.
background normalization: Removal of the background by some image processing technique to estimate the background image and then dividing or subtracting the background from an original image. The technique is useful for when the background is non-uniform. The images below illustrate this where the first shows the input image, the second is the background estimate obtained by dilation with ball
 |
 |
 |
backlighting: A method of illuminating a scene where the background receives more illumination than the foreground . Commonly this is used to produce silhouettes of opaque objects against a lit background, for easier object detection.
bandpass filter: A signal processing filtering technique that allows signals between two specified frequencies to pass but cuts out signals at all other frequencies.
back-propagation: One of the best-studied neural network training algorithms for supervised learning . The name arises from using the propagation of the discrepancies between the computed and desired responses at the network output back to the network inputs. The discrepancies are one of the inputs into the network weight recomputation process.
back-tracking: A basic technique for graph searching : if a terminal but non-solution node is reached, search does not terminate with failure, but continues with still unexplored children of a previously visited non-terminal node. Classic back-tracking algorithms are breadth-first, depth-first, and A* . See also graph , graph searching , search tree .
bar: A raw primal sketch primitive that represents a dark line segment against a lighter background (or its inverse). Bars are also one of the primitives in Marr's theory of vision. The following is a small dark bar observed inside a receptive field :
 |
bar detector: 1) Method or algorithm that produces maximum excitation when a bar is in its receptive field . 2) Device used by thirsty undergraduates.
bar-code reading: Methods and algorithms used for the detection, imaging and interpretation of black parallel lines of different widths arranged to give details on products or other objects. Bar codes themselves have many different coding standards and arrangements. An example bar code is:
 |
barrel distortion: Geometric lens distortion in an optical system that causes the outlines of an object to curve outward, forming a barrel shape. See also pincushion distortion.
barycentrum: See center of mass.
bas-relief ambiguity: The ambiguity in reconstructing a 3D object with Lambertian reflectance using shading from an image under orthographic projection. If the true surface is
baseline: Distance between two cameras used in a binocular stereo system.
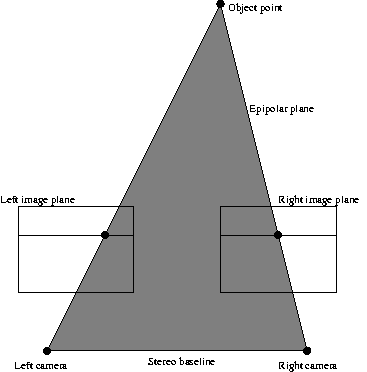 |
basis function representation: A method of representing a function as a sum of simple (usually orthonormal ) ones. For example the Fourier transform represents functions as a weighted sum of sines and cosines.
Bayes' rule: The relationship between the conditional probability of event A given B and the conditional probability of event B given event A. This expressed as
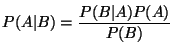
Bayesian classifier: A mathematical approach to classifying a set of data, by selecting the class most likely to have generated that data. If
Bayesian filtering: A probabilistic data fusion technique. It uses a formulation of probabilities to represent the system state and likelihood functions to represent their relationships. In this form, Bayes' rule can be applied and further related probabilities deduced.
Bayesian model: A statistical modeling technique based on two input models:
- a likelihood model
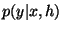 , describing the density of observing
, describing the density of observing 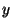 given
given 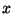 and
and 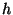 . Regarded as a function of
. Regarded as a function of 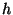 , for a fixed
, for a fixed 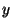 and
and 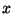 , the density is also known as the likelihood of
, the density is also known as the likelihood of 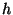 .
.
- a prior model,
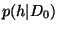 which specifies the a priori density of
which specifies the a priori density of 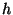 given some known information denoted by
given some known information denoted by 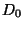 before any new data are taken into account.
before any new data are taken into account.
Bayesian model learning: See probabilistic model learning .
Bayesian network: A belief modeling approach using a graph structure. Nodes are variables and arcs are implied causal dependencies and are given probabilities. These networks are useful for fusing multiple data (possibly of different types) in a uniform and rigorous manner.
BDRF: See bidirectional reflectance distribution function .
beam splitter: An optical system that divides unpolarized light into two orthogonally polarized beams, each at
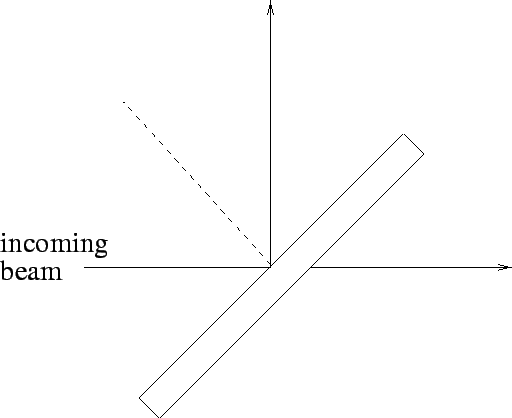 |
behavior analysis: Model based vision techniques for identifying and tracking behavior in humans. Often used for threat analysis.
behavior learning: Generation of goal-driven behavior models by some learning algorithm, for example reinforcement learning.
Beltrami flow: A noise suppression technique where images are treated as surfaces and the surface area is minimized in such a way as to preserve edges. See also diffusion smoothing .
bending energy: 1) A metaphor borrowed from the mechanics of thin metal plates. If a set of landmarks is distributed on two infinite flat metal plates and the differences in the coordinates between the two sets are vertical displacements of the plate, one Cartesian coordinate at a time, then the bending energy is the energy required to bend the metal plate so that the landmarks are coincident. When applied to images, the sets of landmarks may be sets of features. 2) Denotes the amount of energy that is stored due to an object's shape.
best next view: See next view planning .
Bhattacharyya distance: A measure of the (dis)similarity of two probability distributions. Given two arbitrary distributions
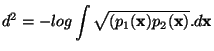
bicubic spline interpolation: A special case of surface interpolation that uses cubic spline functions in two dimensions. This is like bilinear surface interpolation except that the interpolating surface is curved, instead of flat.
bidirectional reflectance distribution function (BRDF/BRDF): If the energy arriving at a surface patch, denoted
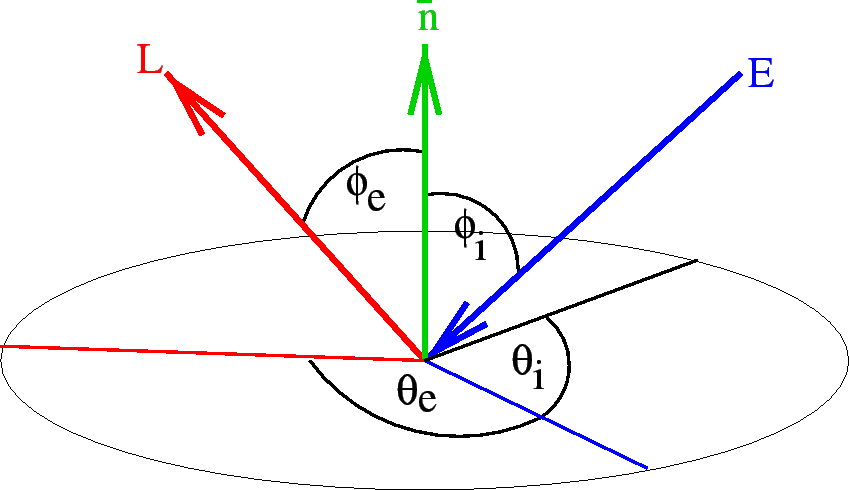 |
bilateral filtering: A non-iterative alternative to anisotropic filtering where images can be smoothed but edges present in them are preserved.
bilateral smoothing: See bilateral filtering.
bilinear surface interpolation: To determine the value of a function
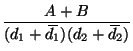
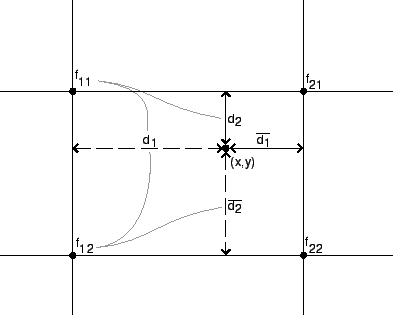 |
bilinearity: A function of two variables
bimodal histogram: A histogram with two pronounced peaks, or modes. This is a convenient intensity histogram for determining a binarizing threshold. An example is:
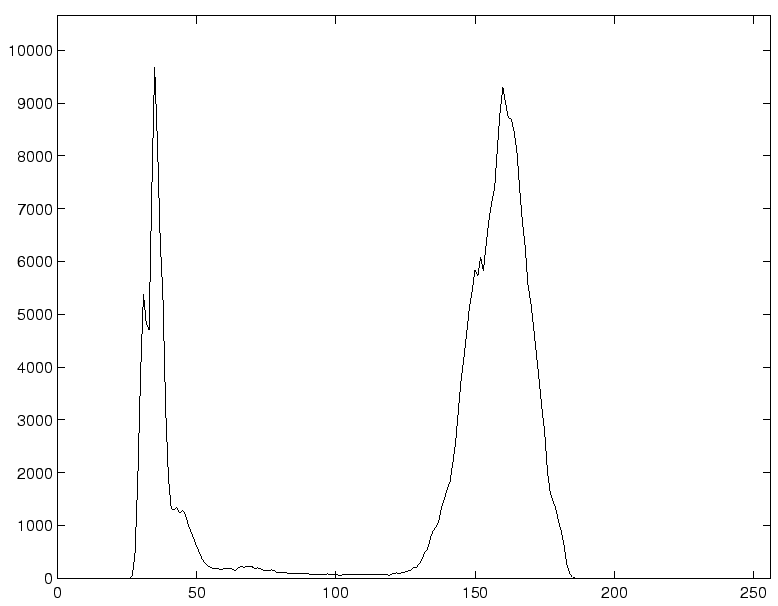 |
bin-picking: The problem of getting a robot manipulator equipped with vision sensors to pick parts, for instance screws, bolts, components of a given assembly, from a random pile. A classic challenge for hand-eye robotic systems, involving at least segmentation , object recognition in clutter and pose estimation .
binarization: See thresholding .
binary image: An image whose pixel s can either be in an 'on' or 'off' state, represented by the integers 1 and 0 respectively. An example is:
 |
binary mathematical morphology: A group of shape-based operations that can be applied to binary images, based around a few simple mathematical concepts from set theory. Common usages include noise reduction , image enhancement and image segmentation . The two most basic operations are dilation and erosion . These operators take two pieces of data as input: the input binary image and a structuring element (also known as a kernel). Virtually all other mathematical morphology operators can be defined in terms of combinations of erosion and dilation along with set operators such as intersection and union. Some of the more important are opening , closing and skeletonization . Binary morphology is a special case of gray scale mathematical morphology . See also mathematical morphology.
binary moment: Given a binary image
binary noise reduction: A method of removing salt-and-pepper noise from binary images. For example, a point could have its value set to the median value of its eight neighbors.
binary object recognition: Model based techniques and algorithms used to recognize objects from their binary images .
binary operation: An operation that takes two images as inputs, such as image subtraction .
binary region skeleton: See skeleton .
binocular: A system that has two cameras looking at the same scene simultaneously usually from a similar viewpoint. See also stereo vision .
binocular stereo: A method of deriving depth information from a pair of calibrated cameras set at some distance apart and pointing in approximately the same direction. Depth information comes from the parallax between the two images and relies on being able to derive the same feature in both images.
binocular tracking: A method that tracks objects or features in 3D using binocular stereo .
biometrics: The science of discriminating individuals from accurate measurement of their physical features. Example biometric measurements are retinal lines, finger lengths, fingerprints, voice characteristics and facial features.
bipartite matching: Graph matching technique often applied in model based vision to match observations with models or stereo to solve the correspondence problem . Assume a set
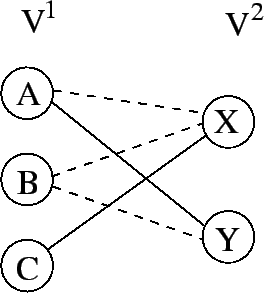 |
bit map: An image with one bit per pixel.
bit-plane encoding: An image compression technique where the image is broken into bit planes and run length coding is applied to each plane. To get the bit planes of an 8-bit gray scale image, the picture has a boolean AND operator applied with the binary value corresponding to the desired plane. For example, ANDing the image with 00010000 gives the fifth bit plane.
bitangent: See curve bitangent .
bitshift operator: The bitshift operator shifts the binary representation of each pixel to the left or right by a set number of bit positions. Shifting 01010110 right by 2 bits gives 00010101. The bitshift operator is a computationally cheap method of dividing or multiplying an image by a power of 2. A shift of
blanking: Clearing a CRT or video device. The vertical blanking interval (VBI) in television transmission is used to carry data other than audio and video.
blending operator: An image processing operator that creates a third image
 |
blob analysis: Blob analysis is a group of algorithms used in medical image analysis. There are four steps in the process: derive optimum foreground/background threshold to segment objects from their background; binarize the images by applying a thresholding operation; perform region growing and assign a labels to each discrete group (blob) of connected pixels; extract physical measurements from the blobs.
blob extraction: A part of blob analysis . See connected component labeling .
block coding: A class of signal coding techniques. The input signal is partitioned into fixed-size blocks, and each block is transmitted after translation to a smaller (for compression ) or larger (for error-correction) block size.
blocks world: The blocks world is the simplified problem domain in which much early artificial intelligence and computer vision research was done. The essential feature of the blocks world is the restriction of analysis to simplified geometric objects such as polyhedra and the assumption that geometric descriptions such as image edges can be easily recovered from the image. An example blocks world scene is:
 |
blooming: Blooming occurs when too much light enters a digital optical system. The light saturates CCD pixels, causing charge to overspill into surrounding elements giving either vertical or horizontal streaking in the image (depending on the orientation of the CCD).
Blum's medial axis: See medial axis transform
blur: A measure of sharpness in an image. Blurring can arise from the sensor being out of focus , noise in the environment or image capture process, target or sensor motion , as a side effect of an image processing operation, etc. A blurred image is:
 |
border detection: See boundary detection .
border tracing: Given a pre-labeled (or segmented) image, the border is the inner layer of each region's connected pixel set. It can be traced using a simple 8-connective or 4-connective stepping procedure in a
boundary: A general term for the lower dimensional structure that separates two objects, such as the curve between neighboring surfaces, or surface between neighboring volume.
boundary description: Functional, geometry based or set-theoretic description of a region boundary . For an example, see chain code .
boundary detection: An image processing algorithm that finds and labels the edge pixels between two neighboring image segments after segmentation . The boundary represents physical discontinuities in the scene, for example changes in color, depth, shape or texture.
boundary grouping: An image processing algorithm that attempts to complete a fully connected image-segment boundary from many broken pieces. A boundary might be broken because it is commonplace for sharp transitions in property values to appear in the image as slow transitions, or sometimes disappear due to noise , blurring , digitization artifacts, poor lighting or surface irregularities, etc.
boundary length: The length of the boundary of an object. See also perimeter .
boundary matching: See curve matching .
boundary property: Characteristics of a boundary , such as arc length , curvature , etc.
boundary representation: See boundary description and B-Rep .
boundary segmentation: See curve segmentation.
boundary-region fusion: Region growing segmentation approach where two adjacent regions are merged when their characteristics are close enough to pass some similarity test. The candidate neighborhood for testing similarity can be the pixels lying near the shared region boundary .
bounding box: The smallest rectangular prism that completely encloses either an object or a set of points. The ratio of the length of box sides is often used as a classification metric in model based recognition .
bottom-up: Reasoning that proceeds from the data to the conclusions. In computer vision, describes algorithms that use the data to generate hypotheses at a low level, that are refined as the algorithm proceeds. Compare top-down .
BRDF/BDRF: See bidirectional reflectance distribution function.
breakpoint detection: See curve segmentation .
breast scan analysis: See mammogram analysis .
Brewster's angle: When light reflects from a dielectric surface it will be polarized perpendicularly to the surface normal. The degree of polarization depends on the incident angle and the refractive indices of the air and reflective medium. The angle of maximum polarization is called Brewster's angle and is given by
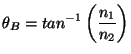
brightness: The quantity of radiation reaching a detector after incidence on a surface. Often measured in lux or ANSI lumens. When translated into an image, the values are scaled to fit the bit patterns available. For example, if an 8-bit byte is used, the maximum value is 255. See also luminance .
brightness adjustment: Increase or decrease in the luminance of an image. To decrease, one can linearly interpolate between the image and a pure black image. To increase, one can linearly extrapolate from a black image and the target. The extrapolation function is
Brodatz texture: A well-known set of texture images often used for testing texture-related algorithms.
building detection: A general term for a specific, model-based set of algorithms for finding buildings in data. The range of data used is large, encompassing stereo images, range images, aerial and ground-level photographs.
bundle adjustment: An algorithm used to optimally determine the three dimensional coordinates of points and camera positions from two dimensional image measurements. This is done by minimizing some cost function that includes the model fitting error and the camera variations. The bundles are the light rays between detected 3D features and each camera center. It is these bundles that are iteratively adjusted (with respect to both camera centers and feature positions).
burn-in: 1) A phenomenon of early tube-based cameras and monitors where, if the same image was presented for long periods of time it became permanently burnt into the phosphorescent layer. Since the advent of modern monitors (1980s) this no longer happens. 2) The practice of shipping only electronic components that have been tested for long periods, in the hope that any defects will manifest themselves early in the component's life (e.g., 72 hours of typical use). 3) The practice of discarding the first several samples of an MCMC process in the hope that a very low-probability starting point will be converge to a high-probability point before beginning to output samples.
butterfly filter: A linear filter designed to respond to "butterfly" patterns in images. A small butterfly filter convolution kernel is