CAD
calculus of variations
calibration object
camera
camera calibration
camera coordinates
camera geometry
camera model
camera motion compensation
camera motion estimation
camera position estimation
Canny edge detector
canonical configuration
cardiac image analysis
cartesian coordinates
cartography
cascaded Hough transform
cascading Gaussians
CAT
catadioptric optics
categorization
category
CBIR
CCD
CCIR camera
cell microscopic analysis
cellular array
center line
center of curvature
center of mass/gravity
center of projection
center-surround operator
central moment
central projection
centroid
certainty representation
chain code
chamfer matching
chamfering
change detection
character recognition
character verification
characteristic view
chessboard distance
Chi-squared distribution
Chi-squared test
chip sensor
chord distribution
chroma
chromatic aberration
chromaticity diagram
chrominance
chromosome analysis
CID
CIE chromaticity coordinates
CIE L*A*B* model
CIE - L*U*V* model
circle
circle detection
circle fitting
circular convolution
circularity
city block distance
classification
classifier
clipping
clique
close operator
clustering/cluster analysis
clutter
CMOS
CMY
CMYB
CMYK
coarse-to-fine processing
coaxial illumination
cognitive vision
coherence detection
coherent fiber optics
coherent light
coincidental alignment
collimate
collimated lighting
collinearity
collineation
color
color based database indexing
color based image retrieval
color clustering
color constancy
color cooccurrence matrix
color correction
color differential invariant
color Doppler
color edge detection
color efficiency
color gamut
color halftoning
color histogram matching
color image
color image restoration
color image segmentation
color indexing
color matching
color mixture model
color model
color moment
color normalization
color quantization
color remapping
color representation system
color space
color temperature
color texture
colorimetry
combinatorial explosion
compactness
compass edge detector
composite filter
composite video
compression
computational theory
computational vision
computer aided design
computer vision
computed axial tomography
concave mirror
concave residue
concavity
concavity tree
concurrence matrix
condensation tracking
condenser lens
conditional dilation
conditional distribution
conditional replenishment
conformal mapping
conic
conic fitting
conic invariant
conical mirror
conjugate direction
conjugate gradient
connected component labeling
connectivity
conservative smoothing
constrained least squares
constrained matching
constrained optimization
constraint satisfaction
constructive solid geometry
content based image retrieval
context
contextual image classification
contextual method
continuous convolution
continuous Fourier transform
continuous learning
contour
contour analysis
contour following
contour grouping
contour length
contour linking
contour matching
contour partitioning
contour representation
contour tracing
contour tracking
contrast
contrast enhancement
contrast stretching
control strategy
convex hull
convexity ratio
convolution
cooccurrence matrix
cooperative algorithm
coordinate system
coordinate system transformation
coplanarity
coplanarity invariant
core line
corner detection
corner feature detector
coronary angiography
correlation
correlation based optical flow estimation
correlation based stereo
correspondence constraint
correspondence problem
cosine diffuser
cosine transform
cost function
covariance
covariance propagation
crack code
crack edge
crack following
Crimmins smoothing
critical motion
cross correlation
cross correlation matching
cross ratio
cross section function
cross-validation
crossing number
CSG
CT
cumulative histogram
currency verification
curse of dimensionality
cursive script recognition
curvature
curvature primal sketch
curvature scale space
curvature sign patch classification
curve
curve normal
curve bitangent
curve evolution
curve fitting
curve inflection
curve invariant
curve invariant point
curve matching
curve normal
curve representation
curve saliency
curve segmentation
curve smoothing
curve tangent vector
cut detection
cyclopean view
cylinder extraction
cylinder patch extraction
cylindrical mosaic
cylindrical surface region
CAD: See computer aided design .
calculus of variations: See variational approach .
calibration object: An object or small scene with easily locatable features used for camera calibration .
 |
camera: 1) The physical device used to acquire images. 2) The mathematical representation of the physical device and its characteristics such as position and calibration. 3) A class of mathematical models of the projection from 3D to 2D, such as affine -, orthographic - or pinhole camera .
camera calibration: Methods for determining the position and orientation of cameras and range sensors in a scene and relating them to scene coordinates. There are essentially four problems in calibration:
- Interior orientation. Determining the internal camera geometry, including its principal point, focal length and lens distortion.
- Exterior orientation. Determining the orientation and position of the camera with respect to some absolute coordinate system.
- Absolute orientation. Determining the transformation between two coordinate systems, the position and orientation of the sensor in the absolute coordinate system from the calibration points.
- Relative orientation. Determining the relative position and orientation between two cameras from projections of calibration points in the scene.
camera coordinates: 1) A viewer-centered representation relative to the camera. The camera coordinate system is positioned and oriented relative to the scene coordinate system and this relationship is determined by camera calibration . 2) An image coordinate system that places the camera's principal point at the origin
camera geometry: The physical geometry of a camera system. See also camera model.
camera model: A mathematical model of the projection from 3D (real world) space to the camera image plane . For example see pinhole camera model .
camera motion compensation: See sensor motion compensation .
camera motion estimation: See sensor motion estimation .
camera position estimation: Estimation of the optical position of the camera relative to the scene or observed structure. This generally consists of six degrees of freedom (three for rotation , three for translation ). It is often a component of camera calibration . Camera position is sometimes called the extrinsic parameters of the camera. Multiple camera positions may be estimated simultaneously with the reconstruction of 3D scene structure in structure-and-motion algorithms.
Canny edge detector: The first of the modern edge detectors . It took account of the trade-off between sensitivity of edge detection versus the accuracy of edge localization. The edge detector consists of four stages: 1) Gaussian smoothing to reduce noise and remove small details, 2) gradient magnitude and direction calculation, 3) non-maximal suppression of smaller gradients by larger ones to focus edge localization and 4) gradient magnitude thresholding and linking that uses hysteresis so as to start linking at strong edge positions, but then also track weaker edges. An example of the edge detection results is:
 |
canonical configuration: A stereo camera configuration in which the optical axes of the cameras are parallel, the baselines are parallel to the image planes and the horizontal axes of the image planes are parallel. This results in epipolar lines that are parallel to the horizontal axes, hence simplifying the search for correspondences.
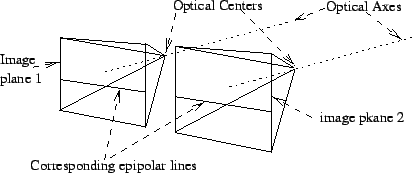 |
cardiac image analysis: Techniques involving the development of 3D vision algorithms for tracking the motion of the heart from NMR and echocardiographic images.
Cartesian coordinates: A position description system where an
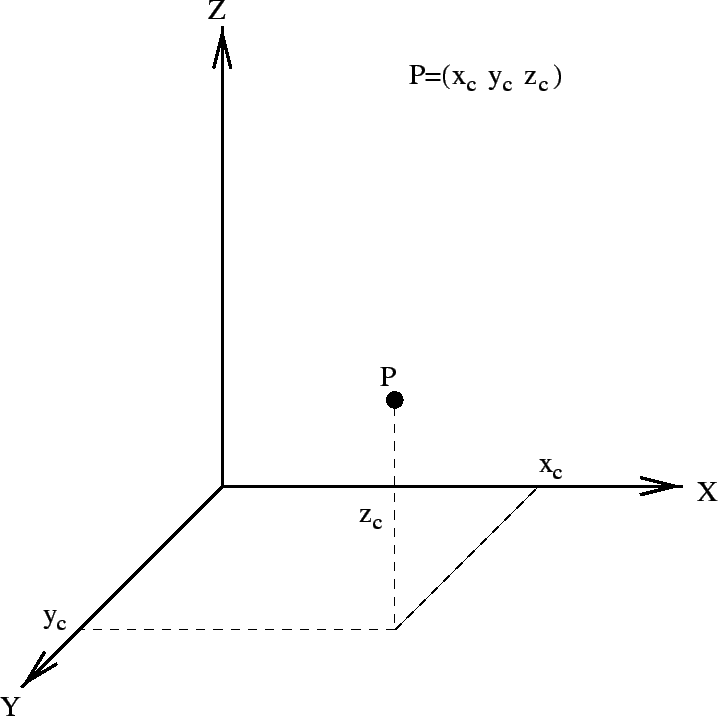 |
cartography: The study of maps and map-building. Automated cartography is the development of algorithms that reduce the manual effort in map building.
cascaded Hough transform: An application of several successive Hough transforms , with the output of one transform used as input to the next.
cascading Gaussians: A term referring to the fact that the convolution of a Gaussian with itself is another Gaussian.
CAT: See X-ray CAT .
catadioptric optics: The general approach of using mirrors in combination with conventional imaging systems to get wide viewing angles (e.g., 180 degrees). It is desirable that a catadioptric system has a single viewpoint because it permits the generation of geometrically correct perspective images from the captured images.
categorization: The subdivision of a set of elements into clearly distinct groups, or categories, defined by specific properties. Also the assignment of an element to a category or recognition of its category.
category: A group or class used in a classification system. For example, in mean and Gaussian curvature shape classification , the local shape of a surface is classified into four main categories: planar, ellipsoidal, hyperbolic, and cylindrical. Another example is the classification of observed grazing animals into one of {sheep, cow, horse}. See also categorization .
CBIR: See content based image retrieval .
CCD: Charge-Coupled Device. A solid state device that can record the number of photons falling on it.
 |
CCIR camera: Camera fulfilling color conversion and pixel formation criteria laid out by the Comité Consultatif International des Radio.
cell microscopic analysis: Automated image processing procedures for finding and analyzing different cell types from images taken by a microscope vision system. Common examples are the analysis of pre-cancerous cells and blood cell analysis.
cellular array: A massively parallel computing architecture, composed of a high number of processing elements. Particularly useful in machine vision applications when a simple 1:N mapping is possible between image pixels and processing elements. See also systolic array and SIMD .
center line: See medial line .
center of curvature: The center of the circle of curvature (or osculating circle) at a point
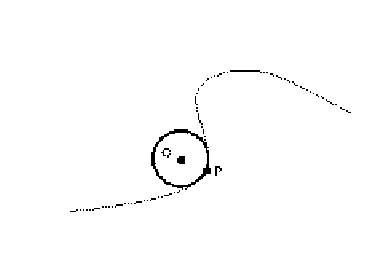 |
center of mass: The point within an object at which the force of gravity appears to act. If the object can be described by a multi-dimensional point set
center of projection: The origin of the camera reference frame in the pinhole camera model . In such a camera, the projection of a point in space is determined by the line passing through the point itself and the center of projection. See:
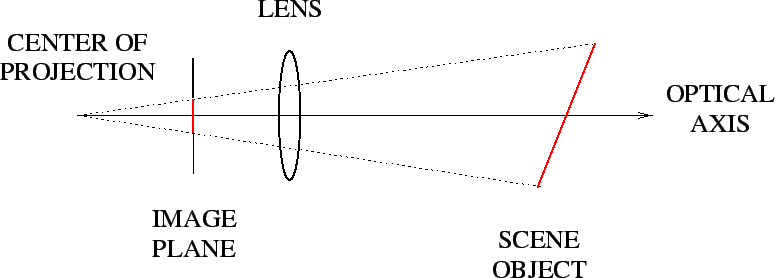 |
center-surround operator: An operator that is particularly sensitive to spot-like image features that have higher (or lower) pixel values in the center than the surrounding areas. A simple convolution mask that can be used as an orientation independent spot detector is:
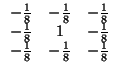
central moments: A family of image moments that are invariant to translation because the center of mass has been subtracted during the calculation. If
central projection: It is defined by projection of an image on the surface of a sphere onto a tangential plane by rays from the center of the sphere. A great circle is the intersection of a plane with the sphere. The image of the great circle under central projection will be a line. Also known as the gnomonic projection.
centroid: See center of mass .
certainty representation: Any of a set of techniques for encoding the belief in a hypothesis, conclusion, calculation, etc. Example representation methods are probability and fuzzy logic .
chain code: An efficient method for contour coding where an arbitrary curve is represented by a sequence of small vectors of unit length in a limited set of possible directions. Depending on whether the 4 connected or the 8 connected grid is employed, the chain code is defined as the digits from 0 to 3 or 0 to 7, assigned to the 4 or 8 neighboring grid points in a counter-clockwise sense. For example, the string 222233000011 describes the small curve shown below using a 4 connected coding scheme, starting from the upper right pixel
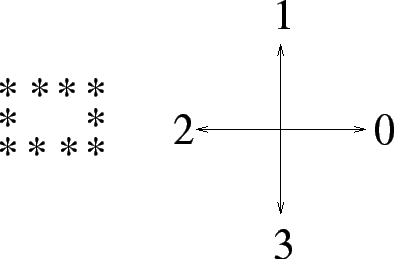 |
chamfer matching: A matching technique based on the comparison of contours, and based on the concept of chamfer distance assessing the similarity of two sets of points. This can be used for matching edge images using the distance transform . See also Hausdorff distance . To find the parameters (for example, translation and scale below) that register a library image and a test image, the binary edge map of the test image is compared to the distance transform. Edges are detected on image 1, and the distance transform of the edge pixels is computed. The edges from image 2 are then matched.
 |
chamfering: See distance transform .
change detection: See motion detection .
character recognition: See optical character recognition .
character verification: A process used to confirm that printed or displayed characters are within some tolerance that guarantees that they are readable by humans. It is used in applications such as labeling.
characteristic view: An approach to object representation in which an object is encoded by a set of views of the object. The views are chosen so that small changes in viewpoint do not cause large changes in appearance (e.g., a singularity event ). Real objects have an unrealistic number of singularities, so practical approaches to creating characteristic views require approximations, such as only using views on a tessellated viewsphere , or only representing the viewpoints that are reasonable stable over large ranges on the viewsphere . See also aspect graph and appearance based recognition .
chess board distance metric: See Manhattan metric .
chi-squared distribution: The chi-squared (
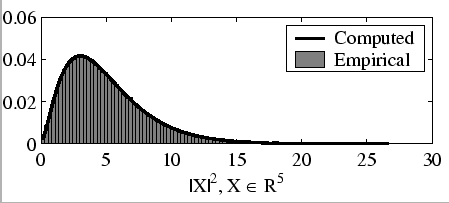 |
chi-squared test: A statistical test of the hypothesis that a set of sampled values has been drawn from a given distribution. See also chi-squared distribution .
chip sensor: A CCD or other semiconductor based light sensitive imaging device.
chord distribution: A 2D shape description technique based on all chords in the shape (that is all pairwise segments between points on the boundary). Histograms of their lengths and orientations are computed. The values in the length histogram are invariant to rotations and scale linearly with the size of object. The orientation histogram values are invariant to scale and shifts.
chroma: The color portion of a video signal that includes hue and saturation , requiring luminance to make it visible. It is also referred to as chrominance .
chromatic aberration: A focusing problem where light of different wavelengths (color) is refracted by different amounts and consequently images at different places. As blue light is refracted more than red light, objects may be imaged with color fringes at places where there are strong changes in lightness .
chromaticity diagram: A 2D slice of a 3D color space . The CIE 1931 chromaticity diagram is the slice through the
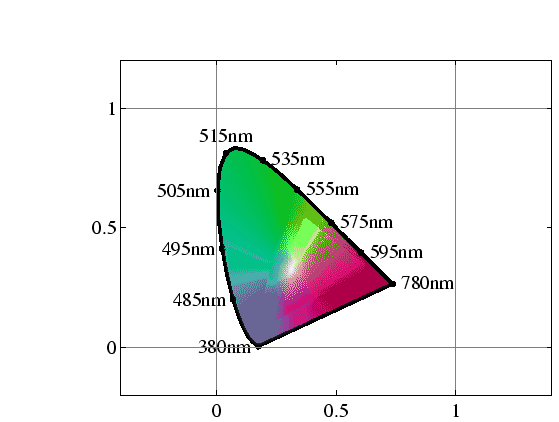 |
chrominance: 1) The part of a video signal that carries color. 2) One or both of the color axes in a 3D color space that distinguishes intensity and color. See also chroma .
chromosome analysis: Vision technique used for the diagnosis of some genetic disorders from microscope images. This usually includes sorting the chromosomes into the 23 pairs and displaying them in a standard chart.
CID: Charge Injection Device. A type of semiconductor imaging device with a matrix of light-sensitive cells. Every pixel in a CID array can be individually addressed via electrical indexing of row and column electrodes. It is unlike a CCD because it transfers collected charge out of the pixel during readout, thus erasing the image.
CIE chromaticity coordinates: Coordinates in the CIE color space with reference to three ideal standard colors
CIE L*A*B* model: A color representation model based on that proposed by the Commission Internationale d'Eclairage (CIE) as an international standard for color measurement. It is designed to be device-independent and perceptually uniform (i.e., the separation between two points in this space corresponds to the perceptual difference between the colors). L*A*B* color consists of a luminance, L*, and two chromatic components: A* component, from green to red; B* component, from blue to yellow. See also CIE L*U*V* model .
CIE L*U*V* model: A color representation system where colors are represented by luminance (L*) and two chrominance components(U*V*). A given change in value in any component corresponds approximately to the same perceptual difference. See also CIE L*A*B* model .
circle: A curve consisting of all points on a plane lying a fixed radius
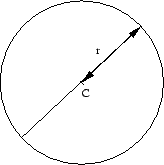 |
circle detection: A class of algorithms, for example the Hough transform , that locate the centers and radii of circles in digital images. In general images, scene circles usually appear as ellipses, as in this example:
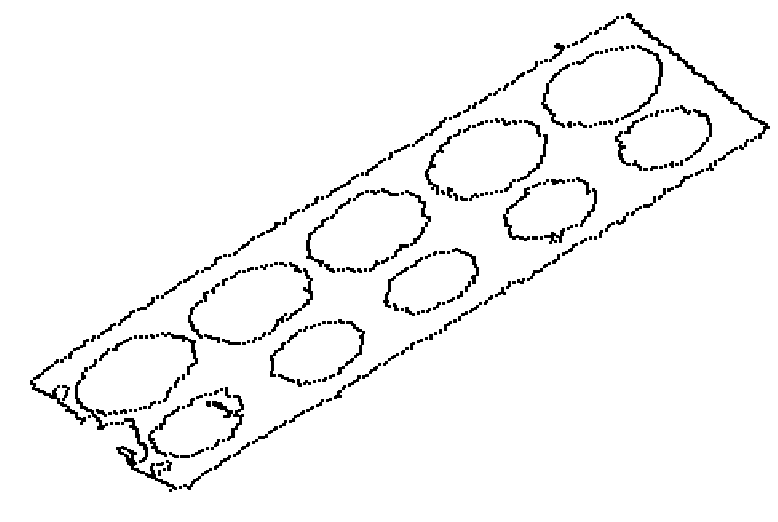 |
circle fitting: Techniques for deriving circle parameters from either 2D or 3D observations. As with all fitting problems, one can either search the parameter space using a good metric (using, for example, a Hough transform ), or can solve a well-posed least-squares problem.
circular convolution: The circular convolution (
circularity: One measure
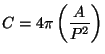
city block distance: See Manhattan metric .
classification: A general term for the assignment of a label (or class) to structures (e.g., pixels, regions , lines , etc.). Example classification problems include: a) labelling pixels as road, vegetation or sky, b) deciding whether cells are cancerous based on cell shapes or c) the person with the observed face is an allowed system user.
classifier: An algorithm assigning a class among several possible to an input pattern or data. See also classification , unsupervised classification , clustering , supervised classification and rule-based classification .
clipping: Removal or non-rendering of objects that do not coincide with the display area.
clique: A clique of a graph
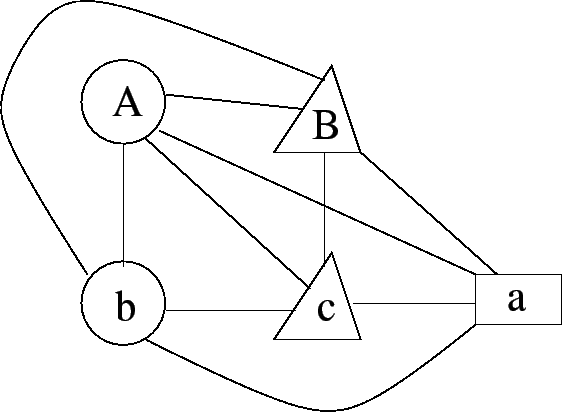 |
close operator: The application of two binary morphology operators, dilation followed by erosion , which has the effect of filling small holes in an image. This figure shows the result of closing with a mask 22 pixels in diameter:
 |
clustering: 1) Grouping together images regions or pixels into larger, homogeneous regions sharing some property. 2) Identifying the subsets of a set of data points
clutter: A generic term for unmodeled or uninteresting elements in an image. For example, a face detector generally has a model for faces, and not for other objects, which are regarded as clutter. The background of an image is often expected to include "clutter". Loosely speaking, clutter is more structured than " noise ".
CMOS: Complementary metal-oxide semiconductor. A technology used in making image sensors and other computer chips.
CMY: See CMYK .
CMYB: See CMYK .
CMYK: Cyan, magenta, yellow and black color model. It is a subtractive model where colors are absorbed by a medium, for example pigments in paints. Where the RGB color model adds hues to black to generate a particular color, the CMYK model subtracts from white. Red, green and blue are secondary colors in this model.
 |
coarse-to-fine processing: Multi-scale algorithm application that begins by processing at a large or coarse level and then, iteratively, to a small or fine level. Importantly, results from each level must be propagated to ensure a good final result. It is used for computing, for example, optical flow.
coaxial illumination: Front lighting with the illumination path running along the imaging optical axis . Advantages of this technique are no visible shadows or direct specularities from the camera's viewpoint.
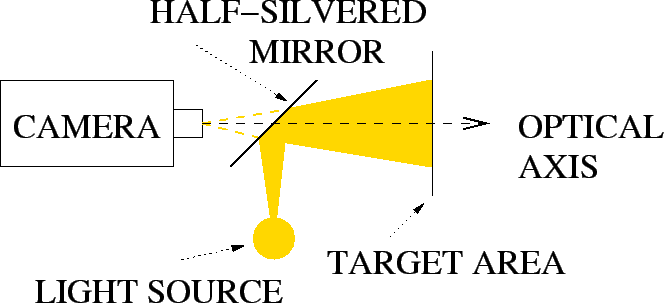 |
cognitive vision: A part of computer vision focusing techniques for recognition and categorization of objects , structures and events, learning and knowledge representation , control and visual attention .
coherence detection: Stereo vision technique where maximal patch correlations are searched for across two images to generate features. It relies on having a good correlation measure and a suitably chosen patch size.
coherent fiber optics: Many fiber optic elements bound into a single cable component with the individual fiber spatial positions aligned, so that it can be used to transmit images.
coherent light: Light , for example generated by a laser , in which the emitted light waves have the same wavelength and are in phase. Such light waves can remain focused over long distances.
coincidental alignment: When two structures seem to be related, but in fact the structures are independent or the alignment is just a consequence of being in some special viewpoint . Examples are random edges being collinear or surfaces coplanar , or object corners being nearby. See also non-accidentalness .
collimate: To align the optics of a vision system, especially those in a telescopic system.
collimated lighting: Collimated lighting (e.g., directional back-lighting) is a special form of structured light. A collimator produces light in which all the rays are parallel.
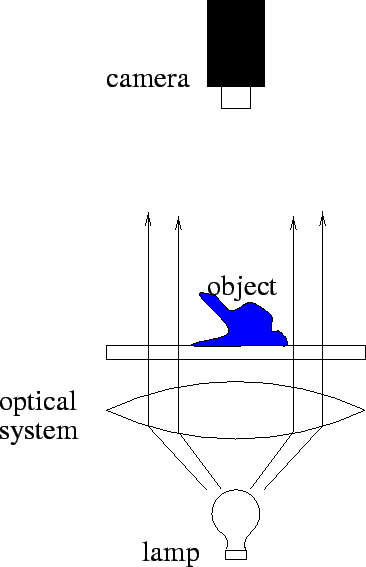 |
collinearity: The property of lying along the same straight line.
collineation: See projective transformation.
color: Color is both a physical and psychological phenomenon. Physically, color refers to the nature of an object texture that allows it to reflect or absorb particular parts of the light incident on it. (See also reflectance .) The psychological aspect is characterized by the visual sensation experienced when light of a particular frequency or wavelength is incident on the retina. The key paradox here concerns why light of slightly different wavelengths should be be so perceptually different (e.g., red versus blue).
color based database indexing: See color based image retrieval .
color based image retrieval: An example of the more general image database indexing process , where one of the main indices into the image database comes from either color samples, the color distribution from a sample image, or by a set of text color terms (e.g., "red"), etc.
color clustering: See color image segmentation.
color constancy: The ability of a vision system to assign a color description to an object that is independent of the lighting environment. This will allow the system to recognize objects under many different lighting conditions. The human vision system does this automatically, but most machine vision systems cannot. For example, humans observing a red object in a cluttered scene under a blue light will still see the object as red. A machine vision system might see it as a very dark blue.
color co-occurrence matrix: A matrix (actually a histogram ) whose elements represent the sum of color values existing, in a given image in a sequence, at a certain pixel position relative to another color existing at a different position in the image. See also co-occurrence matrix .
color correction: 1) Adjustment of colors to achieve color constancy . 2) Any change to the colors of an image. See also gamma correction .
color differential invariant: A type of differential invariant based on color information, such as
color doppler: A method for noninvasively imaging blood flow through the heart or other body parts by displaying flow data on the two dimensional echocardiographic image. Blood flow in different directions will be displayed in different colors.
color edge detection: The process of edge detection in color images. A simple approach is combine (e.g., by addition) the edge strengths of the individual RGB color planes.
color efficiency: A tradeoff that is made with lighting systems, where conflicting design constraints require energy efficient production of light while simultaneously producing sufficiently broad spectrum illumination that the the colors look natural. An obvious example of a skewed tradeoff is with low pressure sodium street lighting. This is energy efficient but has poor color appearance.
color gamut: The subset of all possible colors that a particular display device (CRT, LCD, printer) can display. Because of physical difference in how various devices produce colors, each scanner, display, and printer has a different gamut, or range of colors, that it can represent. The RGB color gamut can only display approximately 70% of the colors that can be perceived. The CMYK color gamut is much smaller, reproducing about 20% of perceivable colors. The color gamut achieved with premixed inks (like the Pantone Matching System) is also smaller than the RGB gamut.
color halftoning: See dithering .
color histogram matching: Used in color image indexing where the similarity measure is the distance between color histograms of two images, e.g., by using the Kullback-Leibler divergence or Bhattacharyya distance .
color image: An image where each element ( pixel ) is a tuple of values from a set of color bases.
color image restoration: See image restoration .
color image segmentation: Segmenting a color image into homogeneous regions based on some similarity criteria. The boundaries around typical regions are shown here:
 |
color indexing: Using color information, e.g., color histograms , for image database indexing . A key issue is varying illumination. It is possible to use ratios of colors from neighboring locations to obtain illumination invariance.
color matching: Due to the phenomenon of trichromacy, any color stimulus can be matched by a mixture of the three primary stimuli. Color matching is expressed as :
color mixture model: A mixture model based on distributions in some color representation system that specifies both the color groups in a model as well as their relationships to each other. The conditional probability of a observed pixel
color models: See color representation system .
color moment: A color image description based on moments of each color channel's histogram , e.g., the mean, variance and skewness of the histograms.
color normalization: Techniques for normalizing the distribution of color values in a color image, so that the image description is invariant to illumination . One simple method for producing invariance to lightness is to use vectors of unit length for color entries, rather than coordinates in the color representation system .
color quantization: The process of reducing the number of colors in a image by selecting a subset of colors, then representing the original image using only them. This has the side-effect of allowing image compression with fewer bits. A color image encoded with progressively fewer numbers of colors is shown here:
 |
color re-mapping: An image transformation where each original color is replaced by another color from a colormap. If the image has indexed colors, this can be a very fast operation and can provide special graphical effects for very low processing overhead.

|
color representation system: A 2D or 3D space used to represent a set of absolute color coordinates. RGB and CIE are examples of such spaces.
color spaces: See color representation system .
color temperature: A scalar measure of colour. 1) The colour temperature of a given colour
color texture: Variations ( texture ) in the appearance of a surface (or region , illumination , etc.) arising because of spatial variations in either the color , reflectance or lightness of a surface.
colorimetry: The measurement of color intensity relative to some standard.
combinatorial explosion: When used correctly, this term refers to how the computational requirements of an algorithm increases very quickly relative to the increase in the number of elements to be processed, as a consequence of having to consider all combinations of elements. For example, consider matching
compactness: A scale , translation and rotation invariant descriptor based on the ratio
compass edge detector: A class of edge detectors based on combining the response of separate edge operators applied at several orientations. The edge response at a pixel is commonly the maximum of the responses over the several orientations.
composite filter: Hardware or software image processing method based on a mixture of components such as noise reduction , feature detection , grouping, etc.
composite video: A television video transmission method created as a backward-compatible solution for the transition from black-and-white to color television. The black-and-white TV sets ignore the color component while color TV sets separate out the color information and display it with the black-and-white intensity.
compression: See image compression .
computational theory: An approach to computer vision algorithm description promoted by Marr. A process can be described at three levels, implementation (e.g., as a program), algorithm (e.g., as a sequence of activities) and computational theory. This third level is characterized by the assumptions behind the process, the mathematical relationship between the input and output process and the description of the properties of the input data (e.g., assumptions of statistical distributions). The claimed advantage of this approach is that the computational theory level makes explicit the essentials of the process, that can then be compared to the essentials of other processes solving the same problem. By this method, the implementation details that can confuse comparisons can be ignored.
computational vision: See computer vision .
computer aided design: 1) A general term for object design processes where a computer assists the designer, e.g., in the specification and layout of components. For example, most current mechanical parts are designed by a computer aided design (CAD) process. 2) A term used for distinguishing objects designed with the assistance of a computer.
computer vision: A broad term for the processing of image data. Every professional will have a different definition that distinguishes computer vision from machine vision , image processing or pattern recognition. . The boundary is not clear, but the main issues that lead to this term being used are more emphasis on 1) underlying theories of optics, light and surfaces, 2) underlying statistical, property and shape models, 3) theory-based algorithms, as contrasted to commercially exploitable algorithms and 4) issues related to what humans broadly relate to "understanding" as contrasted with "automation".
computed axial tomography: Also known as CAT. An X-ray procedure used in conjunction with vision techniques to build a 3D volumetric image from multiple X-ray images taken from different viewpoints . The procedure can be used to produce a series of cross sections of a selected part of the human body, that can be used for medical diagnosis.
concave mirror: The type of mirror used for imaging, in which a concave surface is used to reflect light to a focus. The reflecting surface usually is rotationally symmetric about the optical or principal axis and mirror surface can be part of a sphere , paraboloid, ellipsoid , hyperboloid or other surfaces. It is also known as a converging mirror because it brings light to a focus. In the case of the spherical mirror, half way between the vertex and the sphere center, C, is the mirror focal point, F, as shown here:
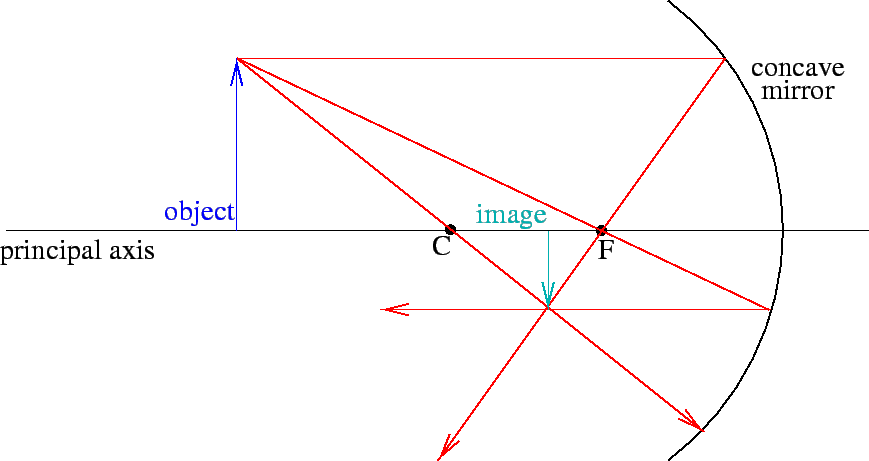 |
concave residue: The set difference between a shape and its convex hull . For a convex shape, the concave residue is empty. Some shapes (in black) and their concave residues (in gray) are shown here:
 |
concavity: Loosely, a depression, dent, hollow or hole in a shape or surface. More precisely, a connected component of a shape's concave residue .
concavity tree: An hierarchical description of an object in the form of a tree. The concavity tree of a shape has the convex hull of its shape as the parent node and the concavity trees of its concavities as the child nodes. These are subtracted from the parent shape to give the original object. The concavity tree of a convex shape is the shape itself. The concavity tree of the gray shape below is shown:
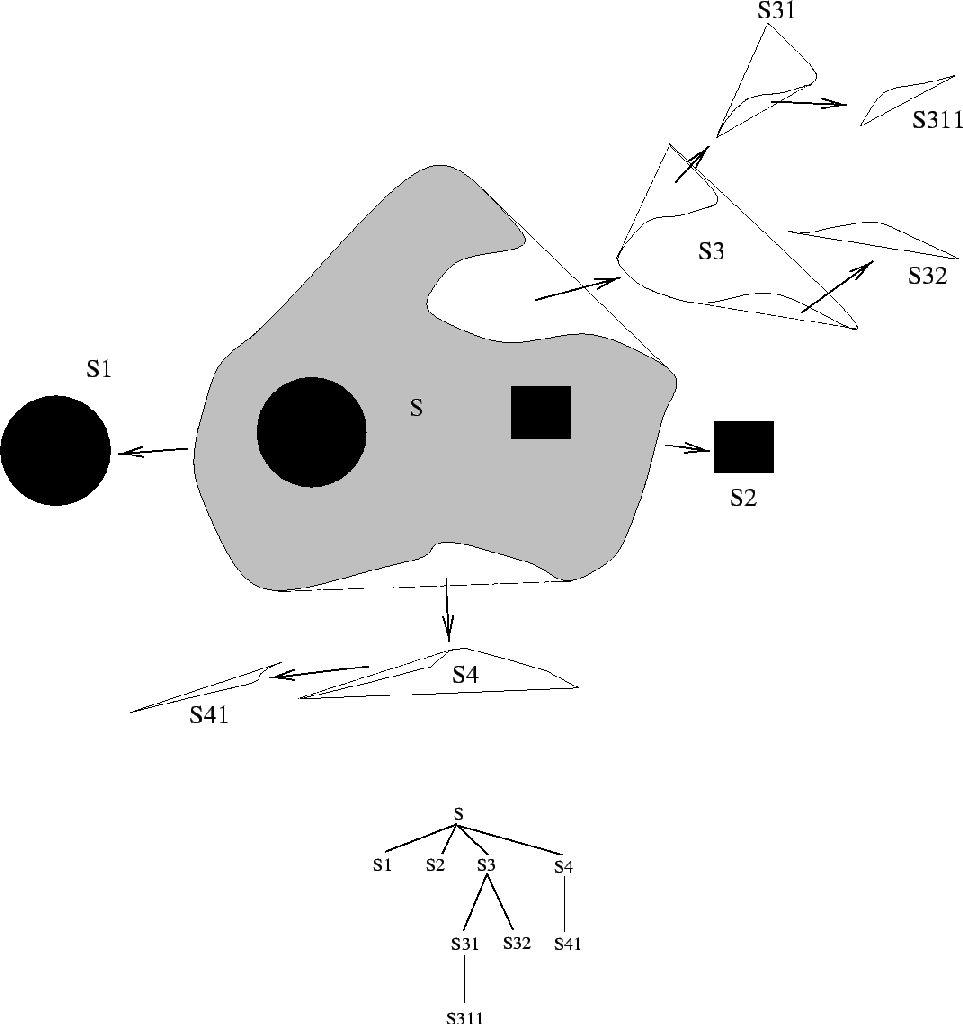 |
concurrence matrix: See co-occurrence matrix .
condensation tracking: Conditional density propagation tracking. The particle filter technique applied by Blake and Isard to edge tracking . A framework for object tracking with multiple simultaneous hypotheses that switches between multiple continuous autoregressive process motion models according to a discrete transition matrix. Using importance sampling it is possible to keep only the
condenser lens: An optical device used to collect light over a wide angle and produce a collimated output beam.
conditional dilation: A binary image operation that is a combination of the dilation operator and a logical AND operation with a mask , that only allows dilation into pixels that belong to the mask. This process can be described by the formula: dilate
conditional distribution: A distribution of one variable given the values of one or more other variables.
conditional replenishment: A method for coding of video signals, where only the portion of a video image that has changed since the previous frame is transmitted. Effective for sequences with largely stationary backgrounds, but more complex sequences require more sophisticated algorithms that perform motion compensation.
conformal mapping: A function from the complex plane to itself,
conic: Curves arising from the intersection of a cone with a plane (also called conic sections). This is a family of curves including the circle, ellipse, parabola and hyperbola. The general form for a conic in 2D is
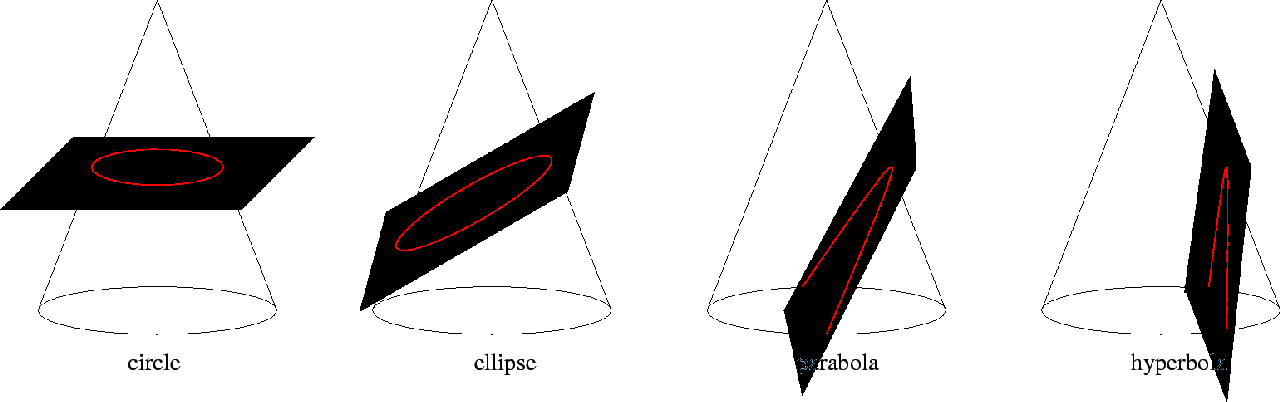 |
conic fitting: The fitting of a geometric model of a conic section
conic invariant: An invariant of a conic section . If the conic is in canonical form
conical mirror: A mirror in the shape of (possibly part of) a cone. It is particularly useful for robot navigation since a camera placed facing the apex of the cone aligning the cone's axis and the optical axis and oriented towards its base can have a full
conjugate direction: Optimization scheme where a set of independent directions are identified on the search space. A pair of vectors
conjugate gradient: A basic technique of numerical optimization in which the minimum of a numerical target function is found by iteratively descending along non-interfering (conjugate) directions . The conjugate gradient method does not require second derivatives and can find the optima of an
connected component labeling: 1) A standard graph problem. Given a graph consisting of nodes and arcs , the problem is to identify nodes forming a connected set. A node is in a set if it has an arc connecting it to another node in the set. 2) Connected component labeling is used in binary and gray scale image processing to join together neighboring pixels into regions. There are several efficient sequential algorithms for this procedure. In this image, the pixels in each connected component have a different color:
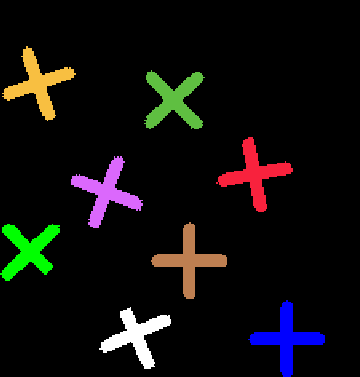 |
connectivity: See pixel connectivity .
conservative smoothing: A noise filtering technique whose name derives from the fact that it employs a fast filtering algorithm that sacrifices noise suppression power to preserve the image detail. A simple form of conservative smoothing replaces a pixel that is larger (smaller) than its 8 connected neighbors by the largest (smallest) value amongst those neighbors. This process works well with impulse noise but is not as effective with Gaussian noise .
constrained least squares: It is sometimes useful to minimize
constrained matching: A generic term for recognition approaches where two objects are compared under a constraint on either or both. One example of this would be a search for moving vehicles under 20 feet in length.
constrained optimization: Optimization of a function
constraint satisfaction: An approach to problem solving that consists of three components: 1) a list of what "variables" need values, 2) a set of allowable values for each "variable" and 3) a set of relationships that must hold between the values for each "variable" (i.e., the constraints). For example, in computer vision, this approach has been used for different structure labelling (e.g., line labelling , region labelling ) and geometric model recovery tasks (e.g., reverse engineering of 3D parts or buildings from range data).
constructive solid geometry (CSG): A method for defining 3D shapes in terms of a mathematically defined set of primitive shapes. Boolean set theoretic operations of intersection, union and difference are used to combine shapes to make more complex shapes. For example:
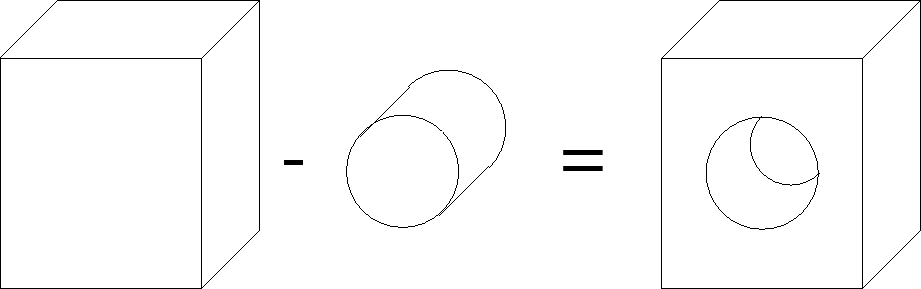 |
content based image retrieval: Image database searching methods that produce matches based on the contents of the images in the database, as contrasted with using text descriptors to do the indexing. For example, one can use descriptors based on color moments to select images with similar invariants.
context: In vision, the elements, information, or knowledge occurring together with or accompanying some data, contributing to the data's full meaning. For example, in a video sequence one can speak of spatial context of a pixel, indicating the intensities at surrounding location in a given frame (image), or of temporal context, indicating the intensities at that pixel location (same coordinates) but in previous and following frames. Information deprived of appropriate context can be ambiguous: for instance, differential optical flow methods can only estimate the normal flow ; the full flow can be estimated considering the spatial context of each pixel. At the level of scene understanding , knowing that the image data comes from a theater performance provides context information that can help distinguish between a real fight and a stage act.
contextual image classification: Algorithms that take into account the source or setting of images in their search for features and relationships in the image. Often this context is composed of region identifiers, color, topology and spatial relationships as well as task-specific knowledge.
contextual method: Algorithms that take into account the spatial arrangement of found features in their search for new ones.
continuous convolution: The convolution of two continuous signals. In 2D image processing terms the convolution of two images
continuous Fourier transform: See Fourier transform .
continuous learning: A general term describing how a system continually updates its model of a process based on current data. For example, updating a background model (for change detection ) as the illumination changes during the day.
contour analysis: Analysis of outlines of image regions.
contour following: See contour linking .
contour grouping: See contour linking .
contour length: The length of a contour in appropriate units of measurements. For instance, the length of an image contour in pixels. See also arc length .
contour linking: Edge detection or boundary detection processes typically identify pixels on the boundary of a region . Connecting these pixels to form a curve is the goal of contour linking.
contour matching: See curve matching .
contour partitioning: See curve segmentation .
contour representation: See boundary representation .
contour tracing: See contour linking .
contour tracking: See contour linking .
contours: See object contour .
contrast: 1) The difference in brightness values between two structures, such as regions or pixels. 2) A texture measure. In a gray scale image , contrast,
![$\displaystyle C = \sum_{i} \sum_{j}(i-j)^{2} P[i,j] $](CVFIG5/img333.png)
contrast enhancement: Contrast enhancement (also known as contrast stretching) expands the distribution of intensity values in an image so that a larger range of sensitivity in the output device can be used. This can make subtle changes in an image more obvious by increasing the displayed contrast between image brightness levels. Histogram equalization is one method of contrast enhancement. An example of contrast enhancement is here:
 |
contrast stretching: See contrast enhancement .
control strategy: The guidelines behind the sequence of processes performed by an automatic image analysis or scene understanding system. For instance, control can be top-down (searching for image data that verifies an expected target) or bottom-up (progressively acting on image data or results to derive hypotheses). The control strategy may allow selection of alternative hypotheses, processes or parameter values, etc.
convex hull: Given a set of points,
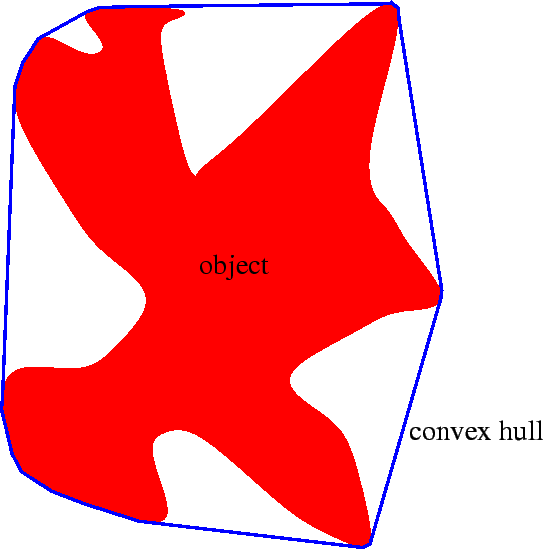 |
convexity ratio: Also known as solidity. A measure that characterizes deviations from convexity. The ratio for shape
convolution operator: A widely used general image and signal processing operator that computes the weighted sum
| +1 | -1 |
 |
co-occurrence matrix: A representation commonly used in texture analysis algorithms. It records the likelihood (usually empirical) of two features or properties being at a given position relative to each other. For example, if the center of the matrix
cooperative algorithm: An algorithm that solves a problem by a series of local interactions between adjacent structures, rather than some global process that has access to all data. The value at a structure changes iteratively in response to changing values at the adjacent structures, such as pixels, lines, regions, etc. The expectation is that the process will converge to a good solution. The algorithms are well suited for massive local parallelism (e.g., SIMD ), and are sometimes proposed as models for human image processing. An early algorithm to solve the stereo correspondence problem used cooperative processing between elements representing the disparity at a given picture element.
coordinate system: A spanning set of linearly independent vectors defining a vector space. One example is the set generally referred to as the X, Y and Z axes. There are, of course, an infinite number of sets of three linearly independent vectors describing 3D space. The right-handed version of this is shown in the figure.
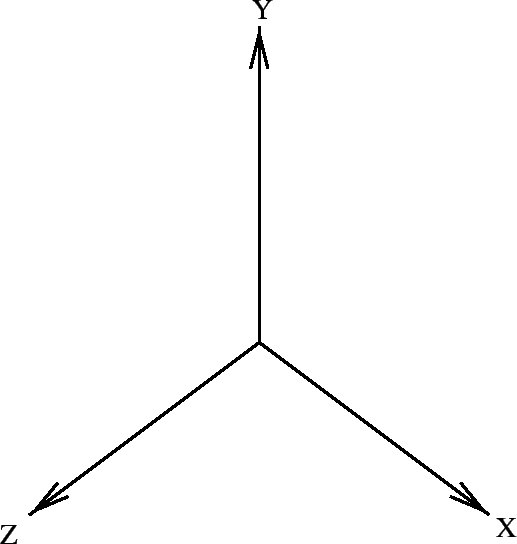 |
coordinate system transformation: A geometric transformation that maps points, vectors or other structures from one coordinate system to another. It is also used to express the relationship between two coordinate systems. Typical transformations include translation and rotation . See also Euclidean transformation.
coplanarity: The property of lying in the same plane. For example, three vectors
coplanarity invariant: A projective invariant that allows one to determine when five corresponding points observed in two (or more) views are coplanar in the 3D space. The five points allow the construction of a set of four collinear points whose cross ratio value can be computed. If the five points are coplanar, then the cross ratio value must be the same in the two views. Here, point A is selected and the lines AB, AC, AD and AE are used to define an invariant cross ration for any line L that intersects them:
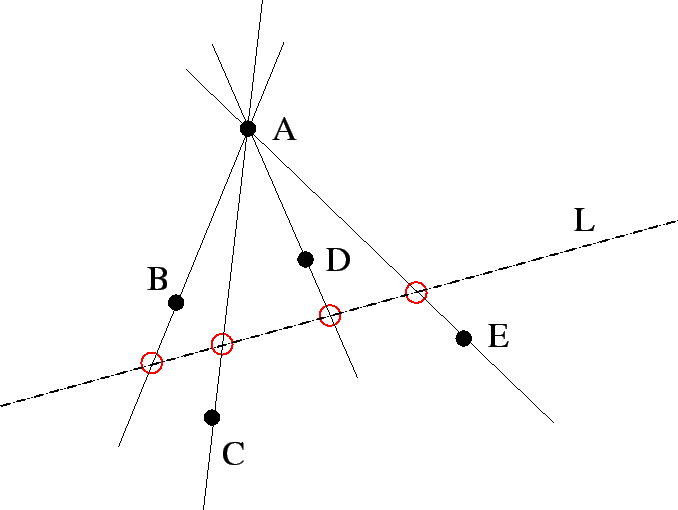 |
core line: See medial line .
corner detection: See curve segmentation .
corner feature detectors: See interest point feature detectors and curve segmentation .
coronary angiography: A class of image processing techniques (usually based on X-ray data) for visualizing and inspecting the blood vessels surrounding the heart (coronaries). See also angiography .
correlation: See cross correlation .
correlation based optical flow estimation: Optical flow estimated by correlating local image texture at each point in two or more images and noting their relative movement.
correlation based stereo: Dense stereo reconstruction (i.e., at every pixel) computed by cross correlating local image neighborhoods in the two images to find corresponding points, from which depth can be computed by stereo triangulation .
correspondence constraint: See stereo correspondence constraint .
correspondence problem: See stereo correspondence problem .
cosine diffuser: Optical correction mechanism for correcting spatial responsivity to light. Since off-angle light is treated with the same response as normal light, a cosine transfer is used to decrease the relative responsivity to it.
cosine transform: Representation of an signal in terms of a basis of cosine functions. For an even 1D function
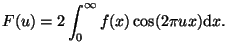
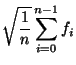 |
|||
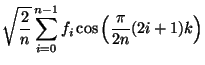 |
For a 2D signal
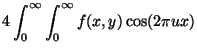
cost function: The function or metric quantifying the cost of a certain action, move or configuration, that is to be minimized over a given parameter space. A key concept of optimization . See also Newton's optimization method and functional optimization .
covariance: The covariance, denoted
For a
covariance propagation: A method of statistical error analysis, in which the covariance of a derived variable can be estimated from the covariances of the variables from which it is derived. For example, assume that independent variables
crack code: A contour description method that codes not the pixels themselves but the cracks between them. This is done as a four-directional scheme as shown below. It can be viewed as a chain code with four directions rather than eight.
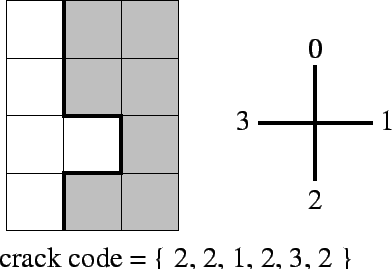 |
crack edge: A type of edge used in line labeling research to represent where two aligned blocks meet. Here, neither a step edge nor fold edge is seen:
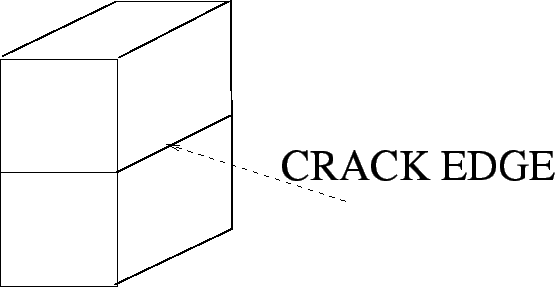 |
crack following: Edge tracking on the dual lattice or "cracks" between pixels based on the continuous segments of line from a crack code .
Crimmins smoothing operator: An iterative algorithm for speckle (salt-and-pepper noise ) reduction. It uses a nonlinear noise reduction technique that compares the intensity of each image pixel with its eight neighbors and either increments or decrements the value to try and make it more representative of its surroundings. The algorithm raises the intensity of pixels that are darker relative to their neighbors and lowers pixels that are relatively brighter. More iterations produce more reduction in noise but at the cost of increased blurring of detail.
critical motion: In the problem of self-calibration of a moving camera, there are certain motions for which calibration algorithms fail to give unique solutions. Sequences for which self-calibration is not possible are known as critical motion sequences.
cross correlation: Standard method of estimating the degree to which two series are correlated. Given two series
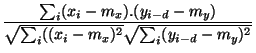
cross correlation matching: Matching based on the cross correlation of two sets. The closer the correlation is to 1, the better the match is. For example, in correlation based stereo , for each pixel in the first image, the corresponding pixel in the second image is the one with the highest correlation score, where the sets being matched are the local neighborhoods of each pixel.
cross ratio: The simplest projective invariant. It generates a scalar from four points of any 1D projective space (e.g., a projective line). The cross ratio for the four points ABCD below is:
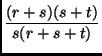
 |
cross section function: Part of the generalized cylinder representation that gives a volumetric based representation of an object. The representation defines the volume by a curved axis, a cross section and a cross section function at each point on that axis. The cross section function defines how the size or shape of the cross section varies as a function of its position along the axis. See also generalized cone . This example shows how the size of the square cross section varies along a straight line to create a truncated pyramid:
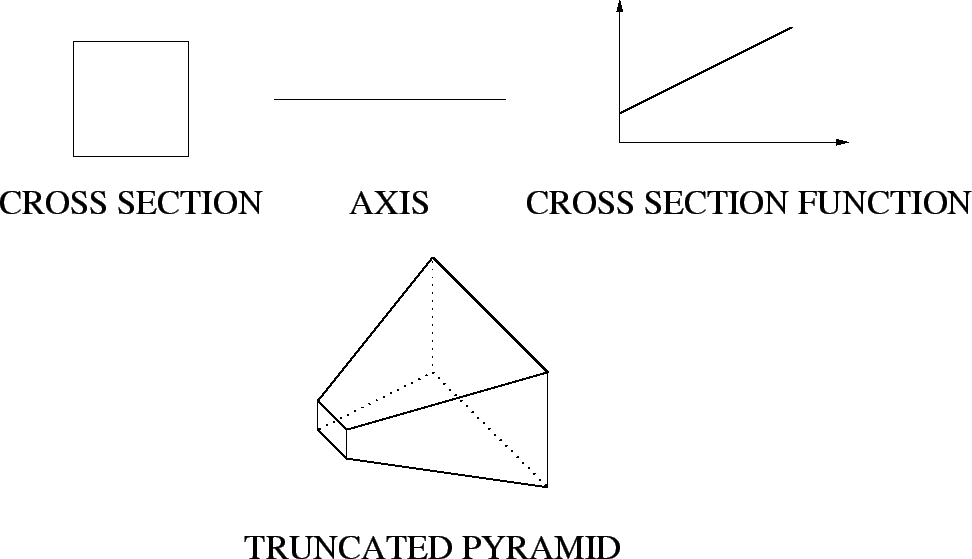 |
cross-validation: A test of how well a model generalizes to other data (i.e., using samples other than those that were used to create the model). This approach can be used to determine when to stop training/learning, before over-generalization occurs. See also leave-one-out test .
crossing number: The crossing number of a graph is the minimum number of arc intersections in any drawing of that graph. A planar graph has crossing number zero. This graph has a crossing number of one:
 |
CSG: See constructive solid geometry
CT: See X-ray CAT .
cumulative histogram: A histogram where the bin contains not only the count of all instances having that value but also the count of all bins having a lower index value. This is the discrete equivalent of the cumulative probability distribution. The right figure is the cumulative histogram corresponding to the normal histogram on the left:
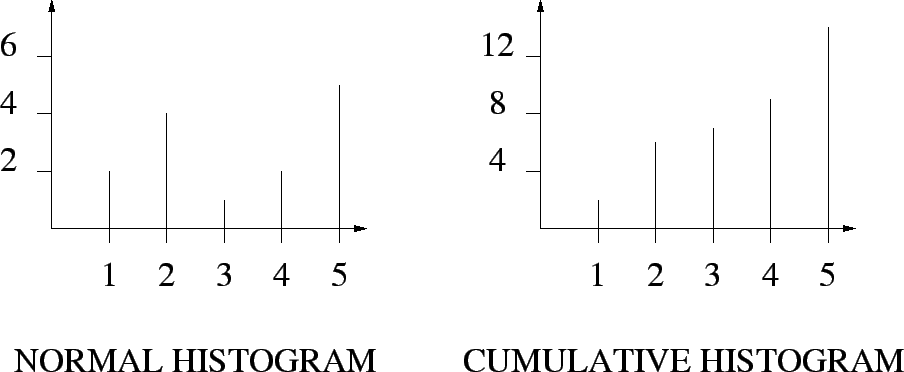 |
currency verification: Algorithms for checking that printed money and coinage are genuine. A specialist field involving optical character recognition.
curse of dimensionality: The exponential growth of possibilities as a function of dimensionality . This might manifest as several effects as the dimensionality increases: 1) the increased amount of computational effort required, 2) the exponentially increasing amount of data required to populate the data space in order that training works and 3) how all data points tend to become equidistant from each other, thus causing problems for clustering and machine learning algorithms.
cursive script recognition: Methods of optical character recognition whereby hand-written cursive (also called joined-up) characters are automatically classified.
curvature: Usually meant to refer to the change in shape of a curve or surface . Mathematically, the curvature
curvature primal sketch: A multi-scale representation of the significant changes in curvature along a planar curve .
curvature scale space: A multi-scale representation of the curvature zero-crossing points of a planar contour as it evolves during smoothing. It is found by parameterizing the contour using arc length, which is then convolved with a Gaussian filter of increasing standard deviation. Curvature zero-crossing points are then recovered and mapped to the scale-space image with the horizontal axis representing the arc length parameter on the original contour and the vertical axis representing the standard deviation of the Gaussian filter.
curvature sign patch classification: A method of local surface classification based on its mean and Gaussian curvature signs, or principal curvature sign class . See also mean and Gaussian curvature shape classification.
curve: A set of connected points in 2D or 3D, where each point has at most two neighbors. The curve could be defined by a set of connected points, by an implicit function (e.g.,
curve binormal: The vector perpendicular to both the tangent and normal vectors to a curve at any given point:
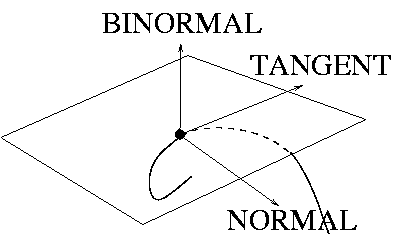 |
curve bitangent: A line tangent to a curve or surface at two different points, as illustrated here:
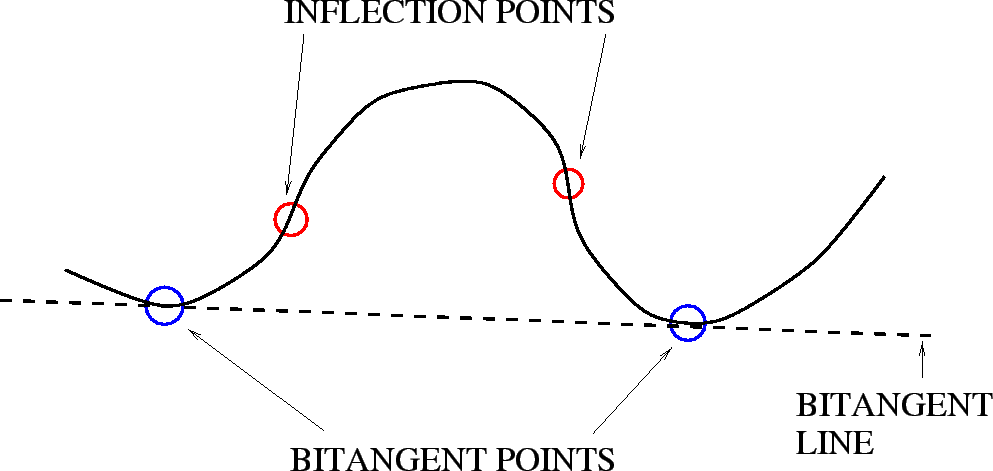 |
curve evolution: A curve abstraction method whereby a curve can be iteratively simplified, as in this example:
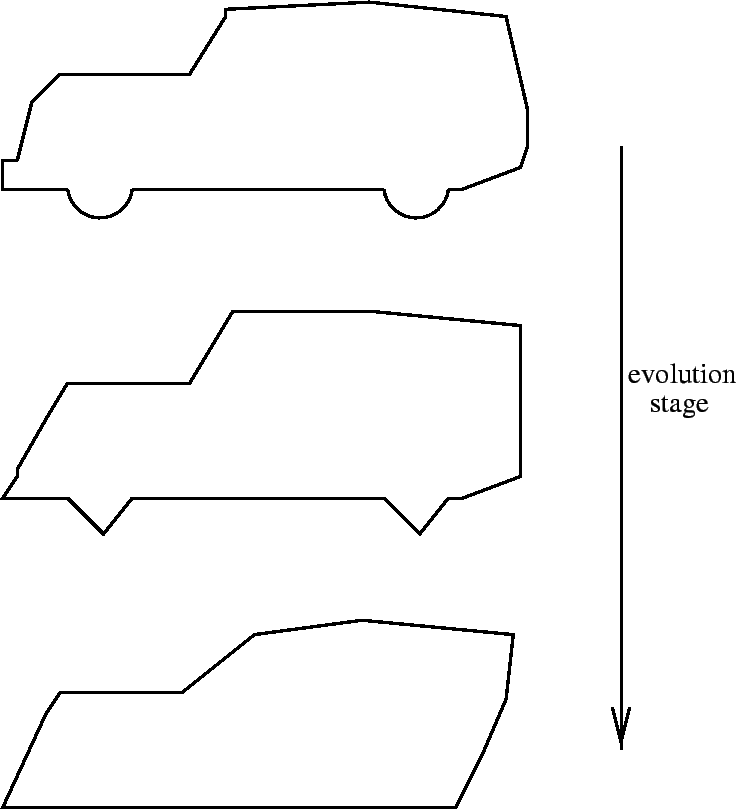 |
curve fitting: Methods for finding the parameters of a best-fit curve through a set of 2D (or 3D) data points. This is often posed as a minimization of the least-squares error between some hypothesized curve and the data points. If the curve,
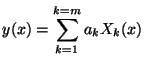
![$\displaystyle \chi^{2} = \sum_{i=1}^{i=N} \left[ \frac{ y_{i} - y(x_{i})}{\sigma_{i}} \right]^2 $](CVFIG5/img401.png)
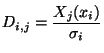
curve inflection: A point on a curve where the curvature is zero as it changes sign from positive to negative, as in the two examples below:
 |
curve invariant: Measures taken over a curve that remain invariant under certain transformations, e.g., arc length and curvature are invariant under Euclidean transformations .
curve invariant point: A point on a curve that has a geometric property that is invariant to changes in projective transformation . Thus, the point can be identified and used for correspondence in multiple views of the same scene. Two well known planar curve invariant points are curvature inflection points and bitangent points, as shown here:
 |
curve matching: The comparison of data sets to previously modeled curves or other curve data sets. If a modeled curve closely corresponds to a data set then an interpretation of similarity can be made. Curve matching differs from curve fitting in that curve fitting involves minimizing the parameters of theoretical models rather than actual examples.
curve normal: The vector perpendicular to the tangent vector to a curve at any given point and that also lies in the plane that locally contains the curve at that point:
 |
curve representation system: Methods of representing or modeling curves parametrically. Examples include: b-splines , crack codes , cross section functions , Fourier descriptors , intrinsic equations, polycurves , polygonal approximations , radius vector functions , snakes , splines , etc.
curve saliency: A voting method for the detection of curves in a 2D or 3D image. Each pixel is convolved with a curve mask to build a saliency map. This map will hold high values for locations in space where likely candidates for curves exist.
curve segmentation: Methods of identifying and splitting curves into different primitive types. The location of changes between one primitive type and another is particularly important. For example, a good curve segmentation algorithm should detect the four lines that make up a square. Methods include: corner detection , Lowe's method and recursive splitting .
curve smoothing: Methods for rounding polygon approximations or vertex-based approximations of surface boundaries. Examples include Bezier curves in 2D and NURBS in 3D. See also curve evolution . An example of a polygonal data curve smoothed by a Bezier curve is:
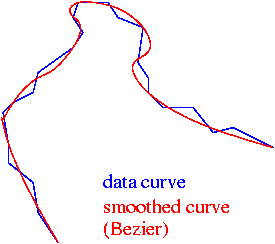 |
curve tangent vector: The vector that is instantaneously parallel to a curve at any given point:
 |
cut detection: The identification of the frames in film or video where the camera viewpoint suddenly changes, either to a new viewpoint within the current scene or to a new scene.
cyclopean view: A term used in stereo image analysis, based on the mythical one-eyed Cyclops. When stereo reconstruction of a scene occurs based on two cameras, one has to consider what coordinate system to use to base the reconstructed 3D coordinates, or what viewpoint to use when presenting the reconstruction. The cyclopean viewpoint is located at the midpoint of the baseline between the two cameras.
cylinder extraction: Methods of identifying the cylinders and the constituent data points from 2.5D and 3D images that are samples from 3D cylinders.
cylinder patch extraction: Given a range image or a set of 3D data points, cylinder patch extraction finds (usually connected) sets of points that lie on the surface of a cylinder, and usually also the equation of that cylinder. This process is useful for detecting and modelling pipework in range images of industrial scenes.
cylindrical mosaic: A photomosaicing approach where individual 2D images are projected onto a cylinder. This is possible only when the camera rotates about a single axis or the camera center of projection remains approximately fixed with respect to the distance to the nearest scene points.
cylindrical surface region: A region of a surface that is locally cylindrical. A region in which all points have zero Gaussian curvature , and nonzero mean curvature.