Bézier Surfaces

This article assumes a basic familiarity with Bézier curves.

A Bézier surface patch is a 4 x 4 grid of 16 control points* which describe a parametric bicubic surface, giving a compact mathematical definition of such a surface without the need to store each of the interpolated points. It is a generalization of the Bézier curve, in which each of four rows of control points can be thought of as a Bézier curve in two dimensions. The Bézier patch representation is powerful for its analytical description of the surface, which may then be easily manipulated.

[* Note that this definition may be generalized to the case of order (n, m) Bézier surfaces with (n + 1)(m + 1) control points. In this article, only the commonly used definition of a 4 x 4 bicubic patch will be discussed.]

I. Definition

A Bézier surface patch is defined by its 4 x 4 Bézier geometry matrix G_B, which specifies the control points of the surface. As in the case of Bézier curves, the corner points of G_B specify actual points on the edge of the interpolated surface, while the “inner” points (any point not on first row, fourth row, first column, or fourth column) are intermediate points which indirectly specify the tangent vectors to the surface. The x, y, and z directions of the surface are calculated independently; thus, for a 3D surface patch, there will actually be separate geometry matrices G_Bx, G_By, and G_Bz, one for each direction. Note that it is possible to represent a Bézier surface in only two dimensions by simply omitting one of the geometric directions. The geometry matrix G_Bk is given by:

G_Bk =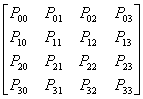

where P_i,j are coordinates in the k direction.

Each point on the surface depends on two parameters u and v which vary between 0 and 1, similar to the case of the 2D Bézier curve. Without loss of generality, let u control the variation along from top to bottom along the patch (i.e. from P_0X to P_3X), and v from left to right (i.e. from P_X0 to P_X3) as specified above. When either u or v is 0 or 1, the point being described lies precisely on the boundary of the surface. Thus, u = v = 0 at control point P₀₀, and u = v = 1 at control point P₃₃.

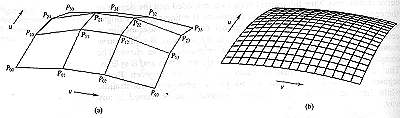
Figure 1: Example of a Bezier surface. At left (a) is the 4 x 4 patch of control points, and at left (b) is the resulting interpolated patch. Figure taken from reference [1] below.

Then, a given point on the surface may be calculated as follows. For each coordinate x, y, and z:

x(u, v) = U · M_B · G_Bx · M_B^T · V^T

y(u, v) = U · M_B · G_By · M_B^T · V^T

z(u, v) = U · M_B · G_Bz · M_B^T · V^T

where M_B is the Bézier basis matrix as used in the calculation of 2D Bézier curves:

M_B =

and the vectors U and V depend on the parameters u and v, which range from 0 to 1:

U = [ u³ u² u 1 ]

V = [ v³ v² v 1 ]

Alternatively (and equivalently), the coordinates of each point on the surface may be calculated directly from the Bernstein basis polynomials. Recall that the Bernstein basis functions are given by the following:

B₀(u) = (1 – u)³

B₁(u) = 3u(1 – u)²

B₂(u) = 3u²(1 – u)

B₃(u) = u³

Then for each of x, y, and z, and given u, v Î [0, 1] as above, a point on the surface is given by:

where is the control point at row i and column j of G_Bk.

Note that the resolution of the interpolated patch depends on how many values of u and v between 0 and 1 are chosen during interpolation. Typically, these values are evenly spaced in the [0, 1] interval.

II. Geometric continuity

As Bézier surfaces are typically used for the representation of objects in three dimensions, geometric continuity at the boundaries between adjoining patches may be an issue. Two kinds of geometric continuity are relevant for discussion here: G⁰ continuity, in which the boundaries of adjoining surfaces align without leaving gaps; and G¹ continuity, in which the tangent vectors at adjoining surfaces must be equal in direction (albeit not magnitude). For G⁰ continuity, two adjoining patches must have identical control points along the shared edge. For G¹ continuity, the two sets of control points on either side of the shared edge must be collinear with the points on the edge (see [3] below).

III. Calculation of surface normals

Given any parametric bicubic surface representation, it is straightforward to calculate the normal to the surface at any point.

The u and v tangent vectors may be calculated separately as follows. For the x direction, the u tangent to the surface is

(U· M_B · G_Bx · M_B^T · V^T) =

[ 3u² 2u 1 0 ] · M_B · G_Bx · M_B^T · V^T

and so on for the y and z components. The v case is similar:

(U· M_B · G_Bx · M_B^T · V^T) =

U · M_B · G_Bx · M_B^T · [ 3v² 2v 1 0 ]^T

Then, the normal to the surface for a given (u, v) is the cross product of the two vectors for each direction, normalized.

IV. Advantages and disadvantages

Bézier surfaces provide a compact way to represent surfaces analytically, allowing explicit control of tangent vectors at each point (and therefore, easy deformation). Parametric bicubic surface definitions easily lend themselves to texture mapping, and for this reason are often used in computer graphics applications.

Problems which may arise in the use of Bézier surface include geometric continuity issues of the kind described above when rendering a complicated surface. Also, rendering of a parametric bicubic patch necessitates the generation of a vertex / polygon representation of the object being rendered. See reference [1] below.

V. References

[1] Bentley, Chris. Rendering Cubic Bézier Patches.

URL: http://www.cs.wpi.edu/~matt/courses/cs563/talks/surface/bez_surf.html

[2] Bourke, Paul. Bézier Surface (in 3D).

URL: http://astronomy.swin.edu.au/~pbourke/surfaces/bezier/

[3] Foley, van Dam, Feiner, and Hughes (1996). Computer Graphics: Principles and Practice (2^nd Edition). New York: Addison-Wesley. pp 478-530.

[4] Wikipedia: Bézier Surfaces.

URL: http://en.wikipedia.org/wiki/B%E9zier_surface

[5] Howe, Denis. Bézier surface.

URL: http://burks.brighton.ac.uk/burks/foldoc/78/11.htm

---

d.donavanik@sms.ed.ac.uk 10 February 2005