This stage of the filtering attempts to identify those locations and scales that are identifiable from different views of the same object. This can be efficiently achieved using a "scale space" function. Further it has been shown under reasonable assumptions it must be based on the Gaussian function. The scale space is defined by the function:
Where * is the convolution operator, G(x, y, σ) is a variable-scale Gaussian and I(x, y) is the input image.
Various techniques can then be used to detect stable keypoint locations in the scale-space. Difference of Gaussians is one such technique, locating scale-space extrema, D(x, y, σ) by computing the difference between two images, one with scale k times the other. D(x, y, σ) is then given by:
To detect the local maxima and minima of D(x, y, σ) each point is compared with its 8 neighbours at the same scale, and its 9 neighbours up and down one scale. If this value is the minimum or maximum of all these points then this point is an extrema.
This stage attempts to eliminate more points from the list of keypoints by finding those that have low contrast or are poorly localised on an edge. This is achieved by calculating the Laplacian, see mathworld.wolfram.com/Laplacian.html for details, value for each keypoint found in stage 1. The location of extremum, z, is given by:
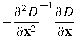
If the function value at z is below a threshold value then this point is excluded. This removes extrema with low contrast. To eliminate extrema based on poor localisation it is noted that in these cases there is a large principle curvature across the edge but a small curvature in the perpendicular direction in the defference of Gaussian function. If this difference is below the ratio of largest to smallest eigenvector, from the 2x2 Hessian matrix at the location and scale of the keypoint, the keypoint is rejected.
This step aims to assign a consistent orientation to the keypoints based on local image properties. The keypoint descriptor, described below, can then be represented relative to this orientation, achieving invariance to rotation. The approach taken to find an orientation is:
- Use the keypoints scale to select the Gaussian smoothed image L, from above
- Compute gradient magnitude, m
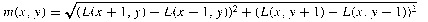
- Compute orientation, θ
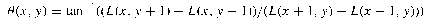
- Form an orientation histogram from gradient orientations of sample points
- Locate the highest peak in the histogram. Use this peak and any other local peak within 80% of the height of this peak to create a keypoint with that orientation
- Some points will be assigned multiple orientations
- Fit a parabola to the 3 histogram values closest to each peak to interpolate the peaks position
The local gradient data, used above, is also used to create keypoint descriptors. The gradient information is rotated to line up with the orientation of the keypoint and then weighted by a Gaussian with variance of 1.5 * keypoint scale. This data is then used to create a set of histograms over a window centred on the keypoint.
Keypoint descriptors typically uses a set of 16 histograms, aligned in a 4x4 grid, each with 8 orientation bins, one for each of the main compass directions and one for each of the mid-points of these directions. This results in a feature vector containing 128 elements.