Pose estimation using the Hough Transform
Philipp Robbel
The Hough Transform is a commonly used method to detect shapes in an
image. The early published work was restricted to the detection of a
number of analytic curves, such as lines or circles, in grey level
images. Here, each sample point from the shape's boundary in the
original image votes for all lines or circles that it may be part of in
a multi-dimensional discretised array, commonly referred to as
accumulator array or Hough space. The dimensionality of the Hough space
is determined by the number of parameters of the analytic curve so that
the 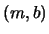 space implied by the line equation
space implied by the line equation 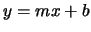 has a dimensionality of two, for example. When multiple points vote for
the same curve, local maxima are gradually built up in Hough space and
may be extracted with a simple thresholding technique.
has a dimensionality of two, for example. When multiple points vote for
the same curve, local maxima are gradually built up in Hough space and
may be extracted with a simple thresholding technique.
An extension of the original algorithm, which supports object
boundaries of arbitrary non-analytic shape, is known as the Generalized
Hough Transform [2].
In the following it is described how the Generalized Hough Transform
may be used for 2D to 2D pose estimation to detect translation and
rotation of a rigid model shape in a test image.
The Generalized Hough Transform does not describe objects as a
parametric curve but instead traverses all the points on the shape's
boundary track. The four-dimensional Hough space is given by the set
where
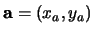 denotes a reference origin for the shape,
denotes a reference origin for the shape, 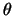 the shape's orientation, and
the shape's orientation, and 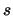 a scalar scaling factor. Before voting can take place in this space, we
construct a table from the model shape that is commonly referred to as
the R-table as follows.
a scalar scaling factor. Before voting can take place in this space, we
construct a table from the model shape that is commonly referred to as
the R-table as follows.
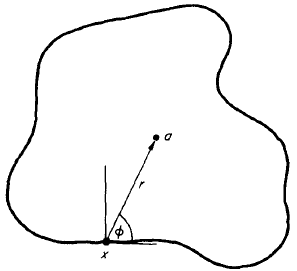
Figure 1:
Finding the displacement vector 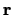 for an arbitrary boundary point
for an arbitrary boundary point 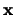 (source: [2]).
(source: [2]).
|
|
First, one has to select an arbitrary fixed reference point 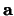 to the model shape, such as the object's centre of mass. For all points
to the model shape, such as the object's centre of mass. For all points 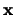 on the boundary, one then stores the vector
on the boundary, one then stores the vector
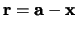 in the R-table, commonly as a function of the gradient
in the R-table, commonly as a function of the gradient 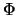 . This process is visualised in Figure 1.
. This process is visualised in Figure 1.
The model vectors stored in the table above can be used to detect the
object in a test image, given that both orientation and scale are
preserved in that image. Since this is generally not the case and since
we would like to detect the shape's pose in the test image, we
construct a number of additional tables for all plausible discretised
values of 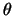 and
and 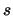 . For both, simple vector operations can be defined on all vectors stored in the original table. If we denote the original R-table by
. For both, simple vector operations can be defined on all vectors stored in the original table. If we denote the original R-table by 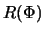 , these scaling and rotation operations are given as follows, resulting in a set of tables
, these scaling and rotation operations are given as follows, resulting in a set of tables 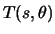 [2].
[2].
Given a test image and the set of R-tables 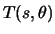 with
with 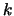 entries each, all points
entries each, all points 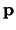 on the test shape's boundary track now vote in the four-dimensional Hough space
on the test shape's boundary track now vote in the four-dimensional Hough space 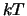 times as follows. For all vectors
times as follows. For all vectors 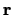 in all tables
in all tables 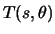 , we vote for the points
, we vote for the points
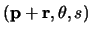 ,
usually by incrementing the respective array entry in Hough space. This
procedure is outlined for an exemplary case with only three
,
usually by incrementing the respective array entry in Hough space. This
procedure is outlined for an exemplary case with only three  vectors in a two-dimensional Hough space (no scaling or rotation of the shape) in Figure 2.
vectors in a two-dimensional Hough space (no scaling or rotation of the shape) in Figure 2.
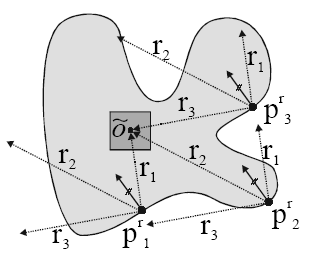
Figure 2:
Reconstruction of the reference origin by adding all displacement vectors 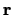 to all boundary points
to all boundary points 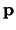 (source: [4]).
(source: [4]).
|
|
After all votes have been cast, we can identify a maximum in Hough space at the point 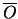 ,
the reconstructed reference origin of the shape. This procedure is
identical for the four-dimensional Hough space when scaling or rotation
is considered.
,
the reconstructed reference origin of the shape. This procedure is
identical for the four-dimensional Hough space when scaling or rotation
is considered.
2D to 2D pose estimation detects translation and rotation of the
(possibly scaled) model shape in the test image. With the procedure
outlined above, we have found the reconstructed reference origin 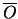 . Since the reference origin in the model shape
. Since the reference origin in the model shape 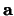 is also available, we can construct the translation vector
is also available, we can construct the translation vector
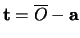 .
.
To obtain the rotational information, we have to find the correct orientation angle 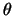 . This information is available from the set of precomputed R-tables
. This information is available from the set of precomputed R-tables 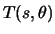 . We choose the angle
. We choose the angle 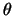 associated with a particular table
associated with a particular table 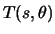 if and only all vectors stored in that table led to the reconstruction of the origin
if and only all vectors stored in that table led to the reconstruction of the origin  .
.
One issue with the technique outlined above is that in general a large
number of candidate scaling factors and rotation angles have to be
considered if no prior knowledge is available to impose bounds on these
values. In [3],
a hardware-accelerated implementation of the Generalized Hough
Transform is described that uses a consumer-class graphics card to run
the exhaustive parameter search on a parallel architecture. An
algorithmic approach to improve the speed of the Generalized Hough
Transform is presented in [4]. Here, a hierarchical strategy is demonstrated that splits the image into a number of tiles that each have associated R-tables.
The idea is that only the first tile has to be associated with an
exhaustive set of tables for all rotations and scaling factors. Once we
have obtained a local maximum in the first tile's accumulator array, we
can pass on this information to the other levels. The inclusion of
invariance in the Generalized Hough Transform is the topic of [1].
The authors describe a method that can extract shapes under similarity
and affine transformations that arise with different 3D orientations of
the target shape relative to the camera position.
- 1
-
A. S. Aguado, E. Montiel, and M. S. Nixon.
Invariant characterisation of the hough transform for pose estimation of arbitrary shapes.
Pattern Recognition, 35(5):1083-1097, 2002.
- 2
-
D. H. Ballard.
Generalizing the hough transform to detect arbitrary shapes.
Pattern Recognition, 13(2):111-122, 1981.
- 3
-
R. Strzodka, I. Ihrke, and M. Magnor.
A graphics hardware implementation of the Generalized Hough Transform for fast object recognition, scale, and 3D pose detection.
In Proceedings of IEEE International Conference on Image
Analysis and Processing (ICIAP'03), pages 188-193, 2003.
- 4
-
M. Ulrich, C. Steger, and A. Baumgartner.
Real-time object recognition using a modified generalized Hough transform.
Pattern Recognition, 36(11):2557-2570, 2003.
Philipp Robbel
2005-02-14
![]() and
and ![]() . For both, simple vector operations can be defined on all vectors stored in the original table. If we denote the original R-table by
. For both, simple vector operations can be defined on all vectors stored in the original table. If we denote the original R-table by ![]() , these scaling and rotation operations are given as follows, resulting in a set of tables
, these scaling and rotation operations are given as follows, resulting in a set of tables ![]() [2].
[2].
![]() . This information is available from the set of precomputed R-tables
. This information is available from the set of precomputed R-tables ![]() . We choose the angle
. We choose the angle ![]() associated with a particular table
associated with a particular table ![]() if and only all vectors stored in that table led to the reconstruction of the origin
if and only all vectors stored in that table led to the reconstruction of the origin ![]() .
.