Supershapes

Many shapes that occur in the real-world are extremely complex in structure. These shapes pose a problem for any computer vision system wishing to model them, as the algorithms used to replicate them can be very complicated and computationally expensive. Therefore research has been carried out into describing these complex shapes in a more compact and efficient manner.

Basic shapes such as circles, squares, ellipses and rectangles are all members of the set of superellipses. Superellipses are defined by:

[x/a]n + [y/b]n = 1


However, the superellipse formula shown above has a very limited symmetry, and so is only useful for representing the most basic shapes. By extending this formula using polar coordinates, and introducing the argument m/4 of the angle φ, we can derive the Superformula:



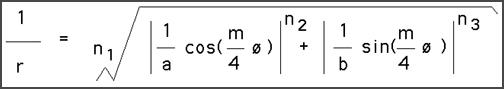
Where r = radius, φ = angle, n1, n2, n3, and m are all Real numbers. a and b are also Real numbers, but excluding 0.

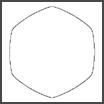
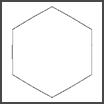
Using the Superformula we can easily create a variety of Supershapes. Values for the variables in the formula have a distinct effect on the shape produced. The higher the value of m, the greater the rotational symmetry will be present in the shape. If m = 0, a circle will be produced. If m = 5 a curved pentagonal shape will result. The value of m effectively divides the plane into m sectors, with a piece of the supershape repeated in each.

m = 0m = 6


The values given to the nx variables change how 'pinched' or 'bloated' the section of the supershape in a sector will be. If the n values are made equal but small, the section of the supershape will be very 'pinched', but retain overall symmetry due to the equality. For large values of n the shapes will be 'bloated', bulging out of the shape found when n1 = n2 = n3 = 1. When n1 is very large, and n2 = n3 are large, geometric supershapes result. If none of the n values are equal, asymmetrical shapes are produced.

m = 6,
n1 = n2 = n3 = 0.3		 m = 6, n1 = 40,
n2 = n3 = 10		 m = 6,
n1 > n2 = n3		 m = 6, n1 = 60,
n2 = 55, n3 = 30


Note: All diagrams were borrowed from Paul Bourke's excellent 'Supershapes (Superformula)' page here.

Extending the Superformula further is a relatively trivial task, yet it makes the formula even more useful to vision related tasks. A 3-dimensional implementation is made possible by using the spherical product:

x = r(θ)cos(θ) r(φ)cos(φ)

y = r(θ)sin(θ) r(φ)cos(φ)

z = r(φ)sin(φ)


where: -π/2 ≤ φ ≤ π/2
and: -π ≤ θ ≤ π


This extension of the Superformula into 3-dimensional space makes modelling almost any object in the real-world a possibility. Not only that, but the computational overheads are relatively small and the mathematics behind the model easy to work with.

Further information on Supershapes can be found at the following locations:

Paul Bourke's 'Supershapes (Superformula)' page,

Paul Bourke's 'Supershape in 3D' page,

'A generic geometric transformation that unifies a wide range of natural and abstract shapes' - J Gielis. Note: There are several publications by Gielis on the subject of supershapes. This one tends to be a lot more useful as an introductory paper, and itself contains references to other relevant material.