Planar Mirrors

  In Solution (16), if we set k = 2 and c > 0, we get the cross-section of a planar mirror:  

$$z \ = \ \frac{c}{2}.$$ (17)

As shown in Figure 2, this plane is the one which bisects the line segment $\vec{\mathbf{v}\mathbf{p}}$ joining the viewpoint and the pinhole.

  

Figure 2: The plane $z=\frac{c}{2}$ is a solution of the fixed viewpoint constraint equation. Conversely, it is possible to show that, given a fixed viewpoint and pinhole, the only planar solution is the perpendicular bisector of the line joining the pinhole to the viewpoint. Hence, for a fixed pinhole, two different planar mirrors cannot share the same effective viewpoint. For each such plane the effective viewpoint is the reflection of the pinhole in the plane. This means that it is impossible to enhance the field of view using a single perspective camera and an arbitrary number of planar mirrors, while still respecting the fixed viewpoint constraint. If multiple cameras are used then solutions using multiple planar mirrors are possible [Nalwa, 1996].

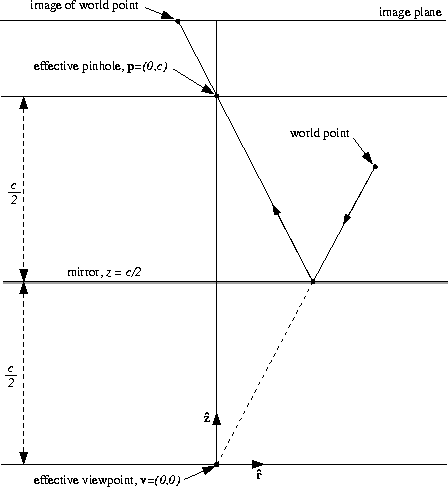The converse of this result is that for a fixed viewpoint $\mathbf{v}$and pinhole $\mathbf{p}$, there is only one planar solution of the fixed viewpoint constraint equation. The unique solution is the perpendicular bisector of the line joining the pinhole to the viewpoint:

$$\left[ \mathbf{x} - \left(\frac{\mathbf{p} + \mathbf{v}}{2}\right)\right] \cdot (\mathbf{p} - \mathbf{v}) \ = \ 0.$$ (18)

To prove this, it is sufficient to consider a fixed pinhole $\mathbf{p}$, a planar mirror with unit normal $\hat\mathbf{n}$,and a point $\mathbf{q}$ on the mirror. Then, the fact that the plane is a solution of the fixed viewpoint constraint implies that there is a single effective viewpoint $\mathbf{v} = \mathbf{v}(\hat\mathbf{n}, \mathbf{q})$. To be more precise, the effective viewpoint is the reflection of the pinhole $\mathbf{p}$ in the mirror; i.e. the single effective viewpoint is:

$$\mathbf{v}(\hat\mathbf{n},\mathbf{q}) \ = \ \mathbf{p} - 2 \... ...{p} - \mathbf{q} ) \cdot \hat\mathbf{n} \right] \hat\mathbf{n}.$$ (19)

Since the reflection of a single point in two different planes is always two different points, the perpendicular bisector is the unique planar solution.

An immediate corollary of this result is that for a single fixed pinhole, no two different planar mirrors can share the same viewpoint. Unfortunately, a single planar mirror does not enhance the field of view, since, discounting occlusions, the same camera moved from $\mathbf{p}$to $\mathbf{v}$ and reflected in the mirror would have exactly the same field of view. It follows that it is impossible to increase the field of view by packing an arbitrary number of planar mirrors (pointing in different directions) in front of a conventional imaging system, while still respecting the fixed viewpoint constraint. On the other hand, in applications such as stereo where multiple viewpoints are a necessary requirement, the multiple views of a scene can be captured by a single camera using multiple planar mirrors. See, for example, [Goshtasby and Gruver, 1993] and [Nene and Nayar, 1998].

This brings us to the panoramic camera proposed by Nalwa [Nalwa, 1996]. To ensure a single viewpoint while using multiple planar mirrors, Nalwa [Nalwa, 1996] arrived at a design that uses four separate imaging systems. Four planar mirrors are arranged in a square-based pyramid, and each of the four cameras is placed above one of the faces of the pyramid. The effective pinholes of the cameras are moved until the four effective viewpoints (i.e. the reflections of the pinholes in the mirrors) coincide. The result is a sensor that has a single effective viewpoint and a panoramic field of view of approximately $360^\circ \times 50^\circ$. The panoramic image is of relatively high resolution since it is generated from the four images captured by the four cameras. This sensor is straightforward to implement, but requires four of each component: i.e. four cameras, four lenses, and four digitizers. (It is possible to use only one digitizer but at a reduced frame rate.)