Noise-resistant affine-invariant skeletons
We give a new definition for affine invariant skeletons of closed planar curves. The goal is to create an skeleton that is invariant respect to translations, rotations and shear strains (see Fig 1). Specifically, if a curve C is transformed by the affine transformation
X'=AX+T
where T is a vector and A is a matrix of unit determinant, then the skeleton S of C will be transformed in the same way. Moreover, we would like the skeleton not to be too sensitive to the noise that may be present on the curve.
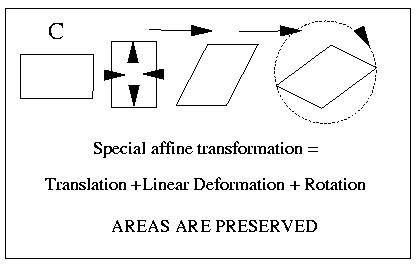
Figure 1
In the classical euclidean definition, the skeleton is the set of points X equidistant from at least two points of the curve C, provided the distances are global minima (see Fig. 2).The euclidean skeleton is invariant respect to euclidean transformations, but is not invariant respect to linear deformations.

Figure 2
In order to create an affine invariant skeleton, we can use a suitable definition for affine invariant distance. In [1] G. Sapiro and P. Giblin used affine geometry and defined the affine distance between a point X and the point C(s) on the curve as d(X,s) = [C(s)-X,C'(s)], where s is the affine arclength and [] represents the z component of the cross product. This expression involves second derivatives of the curve C because s is defined as ds=[Cp, Cpp ]1/3dp, where p is an arbitrary curve parameter. Thus, this distance it is very sensitive to noise, and makes difficult the computation of skeletons with noisy curves.
We can define another affine invariant distance which does not contain derivatives and that is more resistant to noise:
Definition 1: We define the affine distance d(X,s) between a generic point X and a point of the curve C(s) as the area between the curve C and the chord that joins X and C(s) (see Fig. 3). We restrict ourselves to chords which touch the curve exactly twice.
This distance function may have discontinuities, and may also be undefined in some interval of the variable s. However, this definition of distance is much more resistant to noise because the area computation partially averages out the noise on the curve.
In [3] we discuss some properties of the affine distance, hich are valid
for smooth convex curves (see also [2]):
A) If d(X,s) has a local extremum for the chord (C(s),
C(s')) then X is in the middle of that chord.
B) The envelope of the chords cutting off a fixed area (=affine
distance) from C (the affine eroded set) is the locus of midpoints
of the chords.
C) The first two derivatives of d respect to s
vanish at (s,X) if and only if X is the midpoint of the chord
and also the tangents to C at the endpoints of the chord are parallel.

Figure 3
Now we define the skeleton as in the Euclidean case and as in [1].
Definition 2: X is a point of the affine invariant skeleton if and only if there exist two different points C(s1) and C(s2) which define two different chords that contain X and have equal area
provided that these distances are defined and are global minima.
In Fig. 4 we show some affine skeletons which can be computed analytically.
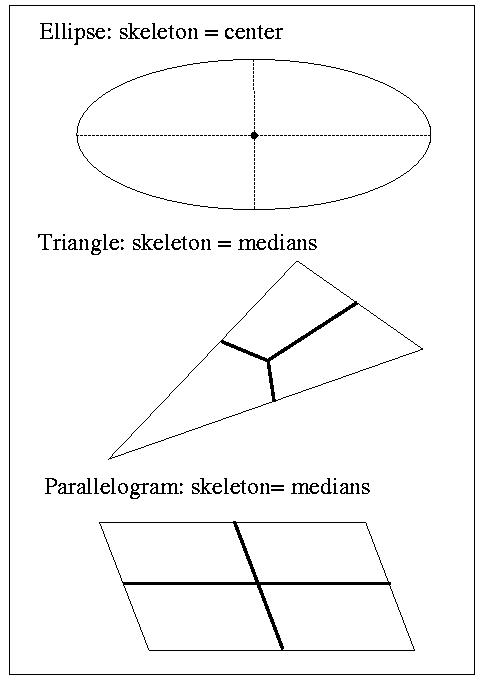
Figure 4
In [3] we propose a numerical implementation of the affine skeleton.
In Fig. 5 we show some examples:
In Fig. 5a we show the skeleton of a triangle, which is analytically
known, and the skeleton after introducing noise. In Fig. 5b we apply an
affine transformation to a curve and we add some noise. The skeleton was
transformed in the same way, and, despite of the noise, the skeleton is
still distinguishable. In Fig. 6 we show the skeleton of curves extracted
from a real image.
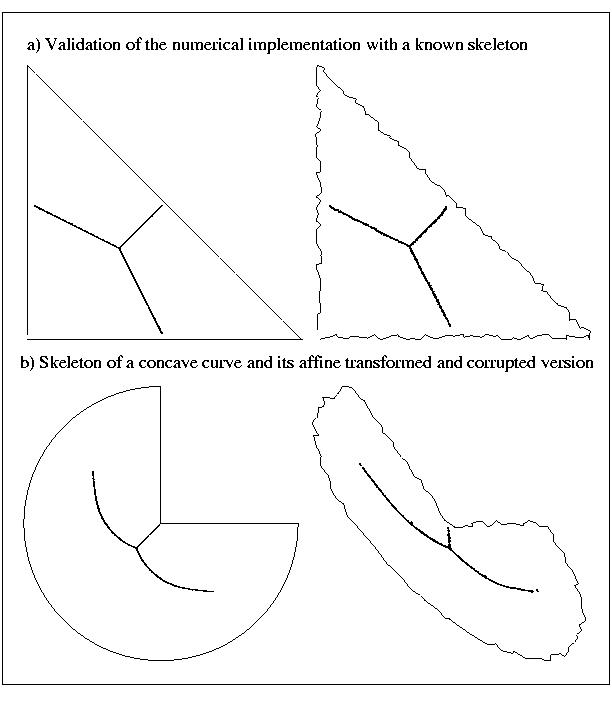
Figure 5

Figure 6
REFERENCES
1- P Giblin and G Sapiro, ``Affine invariant distances, envelopes and symmetry sets'', Geom. Ded. 71, pp. 237-261, 1998.
2- L Moisan, "Affine plane curve evolution: a fully consistent scheme", IEEE Trans on Image Processing, 7 pp. 411-420.
3- S Betelu, G Sapiro, A Tannenbaum and P Giblin, "Noise resistant affine skeletons of planar curves." ECCV2000, Dublin, June 2000.