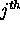 unit is
in the 1 state is
unit is
in the 1 state is 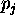 where
where




Boltzmann machines are discrete networks, with input, output and hidden
units, in which the units update their state according to a stochastic
decision rule.
For a given temperature
T, the probability that the 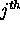 unit is
in the 1 state is
unit is
in the 1 state is 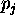 where
where
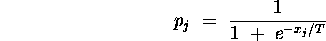
Here, 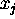 is as usual the
is as usual the 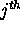 unit input.
unit input.
Note that T = 0 gives a step function for this probability and
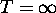 gives a uniform probability of
gives a uniform probability of 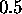 .
.
It can be shown that after a certain time at fixed T,
such networks reach a thermal equilibrium
in which the
probability of a given configuration of units is constant.
Thus, while the precise state of the machine cannot be known, it
is possible to reason about where it `probably' is.
For two such configurations A and B, suppose the respective
energies (measured according to the Hopfield formula)
are 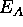 and
and 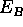 , and the associated probabilities
, and the associated probabilities
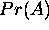 and
and 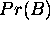 .
It can further be shown that
.
It can further be shown that
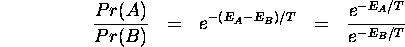
That is, the probabilities follow a Boltzmann distribution. Note that
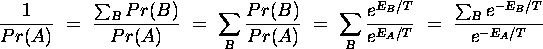
and so
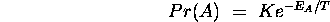
where K is a constant depending on the interconnections, weights and temperature. Thus the state with the lowest energy has the highest probability.
If we gradually reduce T, we have a high probability of achieving a global minimum for the system energy. At high T we locate coarse minima, which are refined as T reduces. This is the important technique of simulated annealing (see Kirkpatrick, Gelatt and Vecchi).
We hope to train the weights 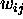 such that when the input
units are held at the appropriate 0,1 values ( clamped)
the output
units display the appropriate output pattern after annealing.
This is done by performing the following cycle the necessary number of
times;
such that when the input
units are held at the appropriate 0,1 values ( clamped)
the output
units display the appropriate output pattern after annealing.
This is done by performing the following cycle the necessary number of
times;
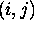 use these
observations to determine
use these
observations to determine
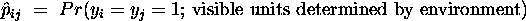
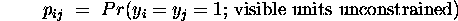
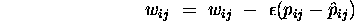
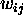 depends only on knowledge of the behaviour of the
depends only on knowledge of the behaviour of the 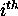 and
and 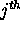 units
- that is, strictly local
behaviour.
units
- that is, strictly local
behaviour.
This result is derived from a measure of the performance of the Boltzmann Machine, much as back-propagation was derived from a measure of the error in a layered network. Since the machine behaves `probabilistically', we need a measure that compares probability distributions; we use the Kullback measure, also called asymmetric divergence.
We suppose that the input and output (or visible)
units may
adopt any one of n states,
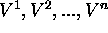 .
Let
.
Let 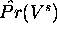 be the probability of state
be the probability of state 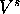 occurring, and let
occurring, and let
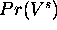 be the probability of observing it in the free
running (unclamped) Boltzmann machine.
We wish
be the probability of observing it in the free
running (unclamped) Boltzmann machine.
We wish 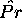 to be the same as Pr, and we measure their similarity
with
to be the same as Pr, and we measure their similarity
with
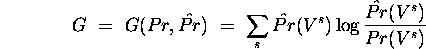
It can be shown that 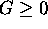 , with equality iff
, with equality iff
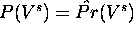 for
for 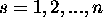 .
The Boltzmann learning procedure works because
.
The Boltzmann learning procedure works because
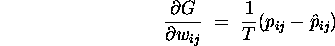
and so we are descending an `error surface',
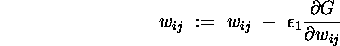
a formula with clear similarities to the gradient descent ideas behind the back propagation learning algorithm.
The learning algorithm above is frequently presented in a simpler form for implementation as follows;
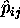 of pair ij being simultaneously 1 `under
environmental control';
set
of pair ij being simultaneously 1 `under
environmental control';
set


The annealing schedule is of critical importance, as is the choice of
the learning constant  .
At high T, too many states are accessible, and at low T too few.
Which T are chosen, and the rate of cooling, will control the success of
the machine.
Bounds has shown for a specific application what the necessary range for
T is.
.
At high T, too many states are accessible, and at low T too few.
Which T are chosen, and the rate of cooling, will control the success of
the machine.
Bounds has shown for a specific application what the necessary range for
T is.



