

Here a robot has to avoid hitting the supports when picking up the block.
A good start on path planning problems can be made if the geometric modeller allows quick computation of the minimum distance betwwen separate objects (or shells in B-rep speak). When this distance gets small, a collision is imminent.

A slight problem here is that we sometimes need distances to get small (or 0):

A bigger problem is that distance on its own may tell us we're about to collide, but it won't tell us where to go next.
Here's another problem: an AGV moving about in a workshop:

We can construct a Voronoi Diagram of the workshop:

This gives each obstruction (including the walls) a territory that is the area of the workshop nearer to that obstruction than to any other. It's not easy to compute, but once we've got it we can do a number of clever things.
Firstly, if the AGV is entirely within one territory, then we only have to worry about distances to the obstacle that owns that territory - all the others are irrelevant. This reduces the size of the problem significantly.
Secondly, if the AGV were a disc and it were to move along the territorial boundaries, it would be as far away from the obstacles as it could be. This might not be far enough, of course, but it's a start on path planning - we move along the territorial boundaries.
But the AGV isn't a disc, and we may still collide with things.
Note that most of the time we only have to be considering two obstacles
- the ones either side of the boundary we're moving along.

Suppose the square can only translate (no rotation), and that it has a reference point, p, defined on it.
Where can p go?

If we grow the obstacle to the shape we'd get if we unioned infinitely many nomads together as p visits every point in the obstacle, the shape we end up with (in this case) is the region p can't visit.
This growing operation is called forming the Minkowski sum of the two sets - obstacle and nomad.
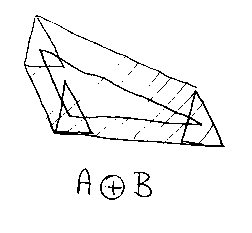
Let's look at calculating the Minkowski sum of two triangles:

The Minkowski sum is written as a + with a circle.
The Minkowski sum of the square and rectangle only worked because the square is symmetrical. In general we need to reflect the nomad in the origin:

before computing the Minkowski sum.
Here is an example that makes this more obvious - a half-disc nomad and a rectangular obstacle.

Here is the place where the reference point on the half-disc can't go - the Minkowski difference of the two shapes:

Here's an example of a Minkowski sum between more complicated shapes - a part of a tape transport mechanism and a disc and triangle:

Note that it is not necessary for either shape to be simply-connected; here the nomad is two separate shapes that move together.
With Minkowski sums, the problem of path planning for a complicated shape just translating reduces to moving a single point through the expanded obstacles. There are a number of ways to do this. We have already seen moving along the edges of the Voronoi territories. Another method is to imagine all the expanded obstacles have an electric charge and to move the point along the lowest potential. This is rather like the optimization we saw in the last chapter and suffers from the same problem of getting stuck in local minima.
But we still don't have rotations, and computing Minkowski sums is still
a research issue for shapes other than polyhedra.
The position of the nomad above when it was translating was decided
by two numbers - the position of the reference point. Let's call
them x' and y'. Together these form a space that is
distinct from the space in which the obstacles and the nomad exist.
The Minkowski difference, placed in this space, shows where the reference
point can't go. This space is called the configuration space
of the system. A point in it represents a single position of everything
invloved.
Suppose we allow the square to rotate as it's moving round the rectangle.

The configuration space is now three-dimensional as we have an angle in addition to x' and y'. Recent research at Bath by my group allows the computation of a configuration-space map for a system like this. This is an extension to the idea of Minkowski difference to include rotations, and is an idea that dates back to pioneering work in the USA around 1980. Here is the configuration space map for the rotating square and rectangle.

At the moment, we can only compute these exactly for polygonal objects (though we can also find an approximation for objects with curved surfaces). But we can have several nomads, allowing a whole machine to be described. The configuration space is now multi-dimensional, of course - there is one dimension for each degree of freedom of each nomad.
Here is an example - two objects (the little green cube is just a flag), the brown one being the nomad - in an initial and a final configuration.


The nomad has six degrees of freedom, so the configuration space map has six dimensions. The two positions above are represented by two points in that 6D space, and the map (where the points can't go) is an unimaginably complicated swirly 6D solid. But we can get the computer to ray-trace in 6D between the two points and find where the ray enters and leaves that 6D solid.


The biggest map like this that we've made is 12 dimensional with several nomads - this is a world first. There is the possibility now of using these maps for path planning - rays can be used to check parts of paths, and it may even be possible to compute multiidimensional Voronoi diagrams. For an animation of a configuration space problem, click here, and for an example of combining this with constraints, click here.
© Adrian Bowyer 1999