
Sculptured Surfaces
Sculptured surfaces are used in geometric modelling to describe all sorts of bendy things like aeroplane wings, car bodies, gas-turbine blades, ship's hulls and so on that can't be described by simple curved surfaces such as cylinders and cones.

The idea behind them is (conceptually at least) quite simple: take a piece of graph paper, label its axes s and t (say) and then define a three-dimensional vector p in (x, y, z) space that is a function of s and t, p(s,t). As s and t vary, p moves about in a bendy sheet in space - the sculptured surface. Each value of s and t gives a point in the sheet in space; the flat (s, t) graph paper has been mapped into the the sculptured surface in (x, y, z). Conventionally, (but not necessarily) the s and t values are allowed to vary between 0 and 1. The bendy grid of lines in the surface that correspond to either keeping t constant and changing s, or keeping s constant and changing t, are called isoparametric lines (Greek: isos - equal), because they are lines for which one parameter stays the same.
How may we construct such a surface?

Here is one way (invented by S.A. Coons in 1967). Start with four parametric curves in space that represent the edges (where s = 0 or 1 and t = 0 or 1):

and the four corner points:

The curves and points may well come from other parts of the geometric model that we want to match (say fuselage data if we're sticking a wing on, or whatever). Alternatively, we can, for example, define four cubic curves by locating the points p wherever we want, and then specifying gradient vectors that we want the surface to have in the s and t directions. (See the end of this chapter for more details of this.)
We want to fill the hole between the four curves with a sculptured surface, p(s,t). To do this, we use the following:

which looks fairly horrendous.
First, what are the functions f(u) and g(u)? (u is a dummy variable that stands for either s or t.) The functions f(u) and g(u) are used to blend one curve into another. f must start at 1 and drop to 0, g must do the opposite. The simplest ones we could have are linear:


The first four terms in the equation for p(s,t) now (I hope) make some sort of sense. We are adding the four curves together, but multiplying them first by weighting functions that cause their influence to wane as we get further away from them.
The reason for the last four terms in the equation involving the corner points is that each corner point is effectively `counted twice' because two curves go through each one. The subtracted terms compensate for this.
Despite its horrendous appearance, it is quite simple to
program a computer to calculate p(s,t).
Now that we can make a sculptured surface, what problems are we likely to encounter?

Firstly, one surface is rarely enough. To make a complete geometric model of an engineering component with complicated surfaces, we will probably have to join patches together. If we join the corners, we get gaps. This is easily fixed by making the parametric curve at the right-hand end of the left patch the same curve as the left-hand end of the right patch.

This will give us patches joining with
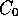 continuity (that is the positions match, but not the gradients).
Suppose we want a smooth
continuity (that is the positions match, but not the gradients).
Suppose we want a smooth 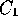 join?
join?

To get this the gradients at the corners of the join have to be co-linear (which is hardly surprising). But also they must have lengths in a constant ratio. If the v and w vectors are the gradients at the corners of the join, then they must obey:

And finally, the blending functions must have gradients of 0 at their ends. The simplest that do this are the cubics:


Machining Sculptured Surfaces
There's obviously no point in going to all this trouble to represent these fancy shapes in the computer if we can't then manufacture them. How do we program, for example, an NC vertical mill to cut a sculptured surface?

If we try to use a cylindrical tool like a slot drill it is very hard to work out where the centre of the bottom of the tool has to be in space so that the edge of the tool is just kissing the surface.
So we use a ball-nosed cutter instead:

Now we have to work out where the centre of the hemispherical end of the cutter is when the spherical surface of the cutter is just touching the sculptured surface. Finding the centre of the cutter is called offsetting.
Consider any point, p, in the surface defined by the two parameter values s and t:

The centre of the sphere needs to be somewhere along the normal vector at right-angles to the surface, n. We need to find n (it will turn out to be convenient if n has a length of 1 as well).
If we take partial derivitives of p with respect to s then t we will get two vectors w and v that are tangents to the surface:

n is obviously at right-angles to w and v.
Recall that the vector product of two vectors is a third vector at right-angles to both of them. Make a vector n':

Take care here: if v and w are in the wrong order, n' will plunge down into the surface (as will the ball nosed cutter that follows it...) instead of sticking out.
We can now make n = n'/ |n'|, which just divides n' by its own length to give n a length of 1. We can now say where the centre of the cutter should be. We take the point on the surface where we want the cutter to touch, p, and add on n multiplied by the radius of the cutter's hemisphere, r:

Having got the cutter to touch one point on the surface, we can now machine the whole surface. We just run the point, p, along a series of very close isoparametric lines in small increments of the non-constant parameter repeatedly doing the calculation just described. This allows us to move the cutting tool so that it just touches the surface:

The result is not perfectly smooth - we end up with a sort-of ploughed-field effect that commonly has to be hand finished. If we keep the parameter increments very fine, then this problem is minimised, but the surface takes longer to machine. In addition we can run a second series of cuts in the other parametric direction:

This leaves a surface with a series of tiny pips, which takes longer, but is easier to hand-finish.
Fitting Sculptured Surfaces to Existing Data
The patch formula due to S.A. Coons has the great virtue that the four edge curves can be any parametric curves you like (they can even have sine and exponential functions in, and so on). However, if you restrict yourself to using 4 cubic curves of the form:

You have 16 coefficients: the a vectors in that equation plus the ones from the three other edge curves.
How can you fit such a patch to some existing data? Well, if you have 16 points in space and you want the patch to pass through them:

You have just enough information to work out the values of those 16 coefficient vectors and to create the sculptured surface. Note that we need 16 points, which includes the 4 in the middle; the 12 round the edge wouldn't be enough.
This is useful if we want to create patches that correspond to some real data that we've gathered - an obvious example would be the points in space that would result from using a coordinate-measuring machine to digitise part of a clay model of a new car.
Often though, we only have the positions of the four corners of the patch that we want. This is clearly not enough to define those 16 coefficients, so what extra data are needed?

We need the pairs of gradient vectors (the partial derivatives of the surface that we encountered in the cutting-tool offsetting problem) at the corners, too. But this still only gives us 12 pieces of information, and we need 16. So in addition second partial derivatives at the corners are required:

We need four vector values for that, one at each corner.
These are called twist vectors, and their influence is rather hard to visualize (though the smaller they are, the flatter the surface is at the corners). They and the magnitudes of the gradient vectors are also hard to define.
However, this scheme does allow patches to be joined edge-to-edge smoothly: all that is required is that the corner points, gradient vectors, and twist vectors match.
© Adrian Bowyer 1996