


Next: Color segmentation
Up: Existing work
Previous: Computational color constancy
Physics-based approaches attempt to derive specific surface reflectance models
based on known physical models of optics and reflection. For instance,
Shafer [27] models surface reflectance as a linear combination of the
diffuse and specular components, and determines the weights of each component
from a measure of specularity. Shafer's Dichromatic Reflectance Model shows that
color variation in 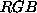 lies with a parallelogram, the length and breadth of
which are determined by the two reflectance components. Klinker [13]
refines the Dichromatic model by showing that surface reflectance
follows a dog-legged (``
lies with a parallelogram, the length and breadth of
which are determined by the two reflectance components. Klinker [13]
refines the Dichromatic model by showing that surface reflectance
follows a dog-legged (``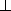 ''-shaped) distribution (within the parallelogram) in
RGB, and then fits a convex polygon to separate the reflectance components.
In a variation of Shafer's approach, Sato [25] uses temporally separated
images to model the surface components. Each of these methods depends on the
presence of pure specular reflection from a point-light source.
Buluswar's Normalized Photometric Function [2] is a simplification
of the Dichromatic model in normalized color space, and determines a photometric
function based on the illuminant size, color, distance between the surface and the
camera, and the surface roughness. This model has been applied to outdoor color
images to estimate the apparent color of an object under daylight.
''-shaped) distribution (within the parallelogram) in
RGB, and then fits a convex polygon to separate the reflectance components.
In a variation of Shafer's approach, Sato [25] uses temporally separated
images to model the surface components. Each of these methods depends on the
presence of pure specular reflection from a point-light source.
Buluswar's Normalized Photometric Function [2] is a simplification
of the Dichromatic model in normalized color space, and determines a photometric
function based on the illuminant size, color, distance between the surface and the
camera, and the surface roughness. This model has been applied to outdoor color
images to estimate the apparent color of an object under daylight.
Lee [16] derives the Neutral Interface Reflectance model which also models
surface reflectance as a linear combination of the two reflectance components and
demonstrated his the effectiveness of his model on spectral power distributions of
surfaces. Unfortunately, Lee stops short of applying his methods to real digital images.
Sato [24] applies the Neutral Interface model and approximates sunlight
as a ``narrow'' Gaussian (with a low standard deviation) to recover the shape
of surfaces in outdoor digital images.
In another approach to determining shape from shading, Nayar [19] uses
photometric sampling (a method of sampling reflectance under varying viewing
geometry) to model hybrid surface reflectance.



Next: Color segmentation
Up: Existing work
Previous: Computational color constancy
Bob Fisher
Wed Mar 31 17:42:48 BST 1999
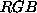 lies with a parallelogram, the length and breadth of
which are determined by the two reflectance components. Klinker [13]
refines the Dichromatic model by showing that surface reflectance
follows a dog-legged (``
lies with a parallelogram, the length and breadth of
which are determined by the two reflectance components. Klinker [13]
refines the Dichromatic model by showing that surface reflectance
follows a dog-legged (``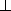 ''-shaped) distribution (within the parallelogram) in
RGB, and then fits a convex polygon to separate the reflectance components.
In a variation of Shafer's approach, Sato [25] uses temporally separated
images to model the surface components. Each of these methods depends on the
presence of pure specular reflection from a point-light source.
Buluswar's Normalized Photometric Function [2] is a simplification
of the Dichromatic model in normalized color space, and determines a photometric
function based on the illuminant size, color, distance between the surface and the
camera, and the surface roughness. This model has been applied to outdoor color
images to estimate the apparent color of an object under daylight.
''-shaped) distribution (within the parallelogram) in
RGB, and then fits a convex polygon to separate the reflectance components.
In a variation of Shafer's approach, Sato [25] uses temporally separated
images to model the surface components. Each of these methods depends on the
presence of pure specular reflection from a point-light source.
Buluswar's Normalized Photometric Function [2] is a simplification
of the Dichromatic model in normalized color space, and determines a photometric
function based on the illuminant size, color, distance between the surface and the
camera, and the surface roughness. This model has been applied to outdoor color
images to estimate the apparent color of an object under daylight.


