Proof of Theorem 1. Let 
be the nearest neighbor
of the query 
in the training set 
. We
show that as long as we independently draw the training samples,
the probability that traverses the recursive partition tree
exactly same as approaches 1 as 
. Assume
at the subregion 
, we have the projection matrices V and
W. The mixture distance from to a center
C under region is
Using the triangle inequality property of the mixture distance, we have
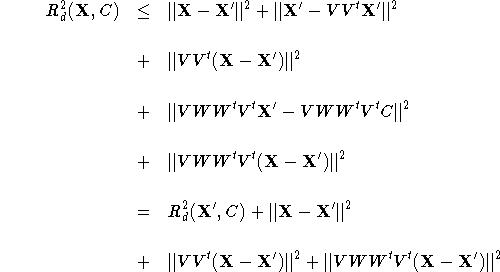
If the sum of the last three terms ( 
)
of the above equation 
, we would have
which means that the approximator would
make the same decision for and . Let 
be the
event that the nearest neighbor of in the training set
has a distance larger than 
while 
denotes
the event that the the nearest neighbor of in the single
has a distance larger than . Since each 
is independently
and identically drawn, we have
On the other hand, is a positively supported, which
means that 
. Thus,
which approaches zero when . So, given any value
and 
, we can have a positive N, so that
for any n>N, we have
Now, we have shown that the approximator makes
the same decision for and as
.
Finally, the fact that is an interior point guarantees that
)=f( 
as .