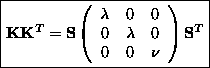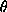 is uniquely determined. However,
is uniquely determined. However, 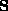 is not. Indeed, if
is not. Indeed, if 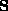 satisfies eq:decomp and
satisfies eq:decomp and  is any invertible matrix which commutes with
is any invertible matrix which commutes with 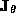 , we have :
, we have :



In eq:decomp, 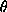 is uniquely determined. However,
is uniquely determined. However, 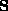 is not. Indeed, if
is not. Indeed, if 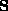 satisfies eq:decomp and
satisfies eq:decomp and  is any invertible matrix which commutes with
is any invertible matrix which commutes with 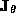 , we have :
, we have :

So, 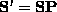 satisfies eq:decomp too.
The converse is also true. That is, if
satisfies eq:decomp too.
The converse is also true. That is, if 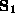 and
and 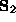 both satisfy eq:decomp, then
both satisfy eq:decomp, then 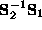 is a matrix which commutes with
is a matrix which commutes with 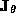 . It can be easily shown that such a matrix can be written :
. It can be easily shown that such a matrix can be written :

Let 
 be an orthogonal matrix such that
be an orthogonal matrix such that 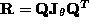 . eq:ginf gives a real Jordan decomposition for
. eq:ginf gives a real Jordan decomposition for 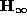 :
:

Furthermore, if  has been calculated by a real Jordan decomposition of
has been calculated by a real Jordan decomposition of  (we will see later how to obtain it), we have, with respect to what has been shown previously, the following relationship :
eq:ambiguity
a,b,c =
(we will see later how to obtain it), we have, with respect to what has been shown previously, the following relationship :
eq:ambiguity
a,b,c =
Then,
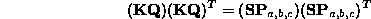
And so, by 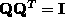 ,
,
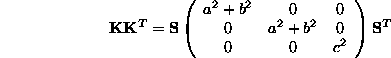
Let be 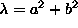 and
and  . We have finally :
. We have finally :
eq:kkt