Conics, quadrics, and superquadrics
Dr Neil Dodgson,
University of Cambridge
Computer Laboratory
The ray tracing primitives have relatively simple mathematical definitions. This is what
makes them attractive: the simple mathematical definition allows for
simple ray-object intersection code. Following from this, it would
seem logical to investigate other shapes with simple mathematical
definitions. Spheres, cones and cylinders are part of a more general
family of parametric surfaces called quadrics (N.B. tori are
not quadrics). Quadrics are the 3D analogue of 2D conics. We
describe these general families below, but it turns out that they are
of little practical use. It would seem that the general quadrics are a
"dead end" in graphics research.
Conics
A conic is a two dimensional curve desribed by the general
equation:
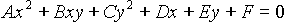
This general form can be rotated, scaled, and translated so that it is
aligned along the axes of the coordinate system. It will then have the
simpler equation:
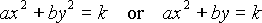
The useful conics are the ellipse (of which the circle is a special
case), the hyperbola, and the parabola. For more details see
R&A section 4-10, especially Table 4-8 on page 242.
Quadrics
The quadrics are the three dimensional analogue of the conics. The
general equation is:
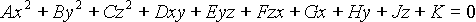
This general form can be rotated, scaled, and translated so that it is
aligned along the axes of the coordinate system. It will then have the
simpler equation:

The useful conics are the ellipsoid (of which the sphere is a special
case), the infinite cylinder, and the infinite cone. Various
hyperboloids, and paraboloids are also defined by these equations, but
these have little real use unless one is designing satellite dishes
(paraboloid), headlamp reflectors (also paraboloid), or power
station cooling towers (hyperboloid). For more details see
R&A section 6-4, especially Figure 6-18 on page 403.
Superquadrics
These are an extension of quadrics, where the power on the coordinate
does not have to be 2. The general form of a superquadric centred at
the origin and aligned along the coordinate axes is:
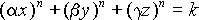
Super-ellipsoids tend to be the only members of this family that are
actually used, and even they are only used in very limited areas. The
effect of n on a super-ellipsoid is roughly as follows:
n=2 is a standard ellipsoid; n<2 is a more pointy
version, the "points" being along the main axes; n>2 becomes
closer to a box as n increases; n=1 is allegedly an
octahedral shape; and n<1 is truly pointy along the main
axes.
The interested student may like to have a quick look at Alan
Barr's two papers on superquadrics. The papers can be found in the Computer
Laboratory library in IEEE Transactions on Computer Graphics and
Applications volume 1, number 1 (January 1981), pages 11-23, and
volume 1, number 3 (July 1981), pages 41-47.
Brian Wyvill describes a use of super-ellipsoids on pages 264 and 265
of "A Computer Animation Tutorial" in Computer Graphics Techniques:
Theory and Practice, Rogers and Earnshaw (editors),
Springer-Verlag, 1990, ISBN 0-387-97237-4.
Source file: p2b.html
Page last updated on Thu Sep 14 16:58:04 BST 2000
by Neil Dodgson
(nad@cl.cam.ac.uk)