The RANSAC (Random Sample Consensus) Algorithm

Robert B. Fisher

The RANSAC algorithm [1] is an algorithm for robust fitting of models in the presence of many data outliers. The algorithm is very simple.

Given a fitting problem with parameters 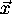tex2html_wrap_inline39, estimate the parameters.

Assume:

  1. The parameters can be estimated from N data items.
  2. There are M data items in total.
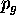  3. The probability of a randomly selected data item being part of a good model is tex2html_wrap_inline45.
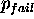  4. The probability that the algorithm will exit without finding a good fit if one exists is tex2html_wrap_inline47.

Then, the algorithm:

  1. selects N data items at random
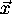
  2. estimates parameter tex2html_wrap_inline39
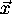  3. finds how many data items (of M) fit the model with parameter vector tex2html_wrap_inline39 within a user given tolerance. Call this K.
  4. if K is big enough, accept fit and exit with success.
  5. repeat 1..4 L times
  6. fail if you get here

How big K has to be depends on what percentage of the data you think belongs to the structure being fit and how many structures you have in the image. If there are multiple structures then, after a successful fit, remove the fit data and redo RANSAC.

You can find L by:

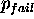tex2html_wrap_inline47 = probability of L consecutive failures
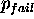tex2html_wrap_inline47 = (prob that a given trial is a failure)tex2html_wrap_inline69
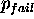tex2html_wrap_inline47 = (1 - prob that a given trial is a success)tex2html_wrap_inline69
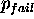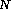tex2html_wrap_inline47 = (1 - (prob that a random data item fits the model)tex2html_wrap_inline77)tex2html_wrap_inline69
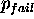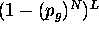
tex2html_wrap_inline47 = tex2html_wrap_inline83

Solve for 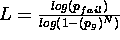tex2html_wrap_inline85.


1
M. A. Fischler, R. C. Bolles. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Comm. of the ACM, Vol 24, pp 381-395, 1981.

Bob Fisher
Mon May 6 18:05:39 BST 2002