
Figure 1: Marr's representational framework
Marr [Mar82] proposed three different levels for the understanding of information processing systems (having vision systems as the target example): computational theory; representation and algorithm; and hardware implementation. One of the Marr's most important contribution was made in the level of representation and algorithm when he proposed a representational framework for vision (Figure 1). He concentrated on the vision task of deriving shape information from images.

Figure 1: Marr's representational framework
It is known that the intensities perceived by any visual system are a
function of four main factors: the geometry (meaning
shape and relative placement); the reflectance of
the visible surfaces; the illumination; and the viewpoint. According to
Marr's theory [Mar82], the early visual system derives
representations in which these factors are separated. The first
2 representations in Marr's framework, the primal sketch and the 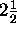 -D sketch, are intended to essentially perform that separation.
-D sketch, are intended to essentially perform that separation.
The detection of intensity changes, the representation and analysis
of local geometric structures and the detection of illumination
effects take place in the process of generation of the primal
sketch. One important principle of the primal sketch is that
independent spatial organizations of the viewed intensities in a scene
reflects the structure of the visible surfaces. Marr proposed to
capture these organizations by using a set of ``place tokens'', or low
level features, which correspond to oriented edges, bars,
ends and blobs, which were represented by a 5-tuple:
( type, position, orientation, scale, contrast). The  -D sketch is intended to represent the orientation and depth of the visible surfaces as well as discontinuities. It is composed of some local surface orientation primitives, distance from the viewer and discontinuities in depth and surface orientation and, as in the previous representation, it is specified in a viewer-centered coordinate system.
-D sketch is intended to represent the orientation and depth of the visible surfaces as well as discontinuities. It is composed of some local surface orientation primitives, distance from the viewer and discontinuities in depth and surface orientation and, as in the previous representation, it is specified in a viewer-centered coordinate system.
The last representation of the Marr's framework is the 3-D model representation. This representation is intended to describe shapes and their organization using a modular and hierarchical organization of volumetric and surface primitives (an example of the organization of shape information in a 3-D model description can be seen in Figure 2). The recognition process uses a catalogue of 3-D models which is a collection of stored 3-D model descriptions and various indices into the collection that allow the association of a new description with the appropriate one in the collection.
All 3-D model descriptions can be organized in a hierarchy according to the specificity of information they carry. The top level of such a hierarchy is a model which does not have a component decomposition and describes the model's principal axis. At the next level in the hierarchy more details are added to the model, like the number and distribution of subcomponent axes along the principal axis. At the lower levels each individual object's model receives more precise descriptions, and they can now be distinguished by the angles and length of their components.
There are three kinds of indices in the model catalogue: specificity index, adjunct index and parent index. The specificity index supports the main recognition process which relates a newly derived 3-D model to a model in the catalogue. The process starts at the top of the hierarchy and searches down the levels through models whose descriptions are consistent with the new model's descriptions until the precision of information in the new model and in the catalogue's model have the same level of specificity. The adjunct and parent indices play a role secondary to that of the specificity index and their purpose is to provide contextual constraints that support the derivation process. The adjunct (or subcomponent) index comes from adjunct relations in a 3-D model and provide access to 3-D models for its components based on their locations, orientations and relative sizes. The inverse of the adjunct index is the parent (or supercomponent) index. The idea behind the parent index is whenever a component of a shape is identified, it can provide information about what the whole shape is likely to be.

Figure 2: An example of Marr's 3-D model description (taken from [Mar82]).
Each box corresponds to a 3-D model. The left side of a box contains the model axis and the right side contains the decomposition of the model's component axes. For illustration purposes only, the relative position and orientation of a model's component axes is incorrectly represented here in a viewer-centered coordinate system, rather than in an object-centered one.
More recently, Watt [Wat88] built a theory about vision based on Marr's theory. Watt reformulated the early visual process interpretation in terms of signal processing filters. However, the main ideas regarding the sketch hypothesis were still maintained.