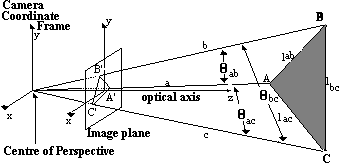
Figure 6:Solving the perspective-3-point problem


We assume that we have identified a group of points in the image, probably junctions between straight lines, but possibly other control points such as ellipse centres which grouping suggests may correspond to similar model control points. Now we have to solve the perspective-n-point problem; i.e. given a set of n corresponding points what is the pose of the object in 3D space ? Usually n is 3 or 4. ( Less than this gives an infinite number of solutions.) When n=3 there are a maximum of eight possible solutions, of which only four occur in real 3D space in front of the camera. If n=4 and these points are coplanar, there is a unique solution; otherwise for non-coplanar points there are two solutions. We shall deal only with the case of 3 points, illustrated in Figure 6, below. We refer mainly to the article by Fischler and Bolles [Reference no 1] although this problem has been discussed by many authors.

The basic problem is to determine the lencths of the three legs of the tetrahedron formed by A,B,C and the centre of perspective CP. From trigonometry, we can form three equations based on the Cosine rule,
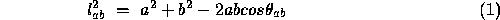
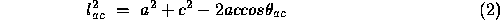

Making the substitutions
i.e. expressing the distances to points B and C as a constant times
the distance to point A, we obtain
It is possible to combine and re-arrange equations 5,6 and 7 to form a quartic equation in
where
(note the G3 in the following corrected equation should be q3):
and
where, either
provided the denominator is not equal to zero, or, if this test fails then
As stated this system of equations has a maximum of eight solutions [See Reference no 1],
but four of these solutions have negative values of a,b and c - they are behind the camera and are isomorphic to the other four solutions which are in the world in front of the camera. Figure 7 gives pictorial example of how these multiple solutions may occur.
Comments to: Sarah Price at ICBL.
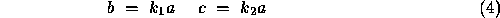
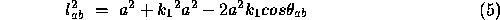
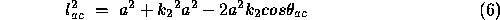

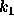 .
.
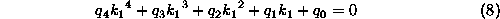
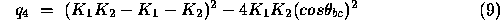
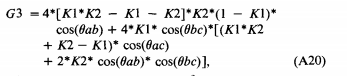
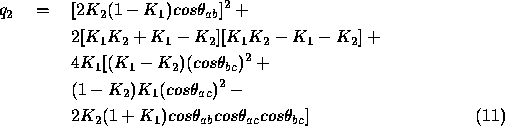
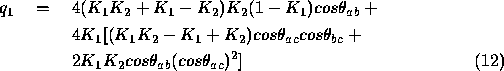
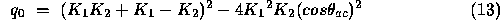
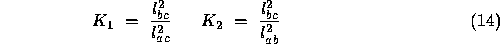
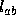 ,
, 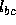 and
and 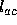 are known from the rigid model of the object, since we have assumed point correspondence.
For each positive real root of the Equation 8 we can then calculate the values of a,b and c, i.e. substituting for k1
in Equation 5, below. This is simply a rearrangement of Equation 5 Then b and c are known directly from Equations 16 and 17 ( i.e. Equation 4). To determine c, we also need to calculate
are known from the rigid model of the object, since we have assumed point correspondence.
For each positive real root of the Equation 8 we can then calculate the values of a,b and c, i.e. substituting for k1
in Equation 5, below. This is simply a rearrangement of Equation 5 Then b and c are known directly from Equations 16 and 17 ( i.e. Equation 4). To determine c, we also need to calculate 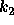 . There are two possible conditions, given in Equations 18 and 19.
. There are two possible conditions, given in Equations 18 and 19.
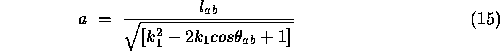


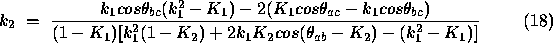
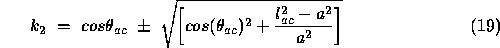
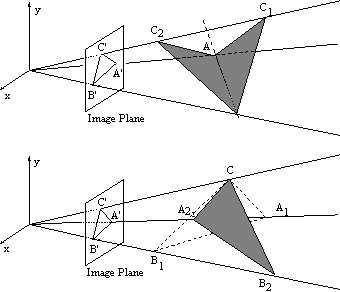
Figure 7: Multiple solutions to the perspective-3-point problem


[ Grouping and non-accidental properties |
Verifying the solution ]