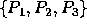 or, alternatively, a matching point
or, alternatively, a matching point 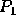 and two vectors
and two vectors 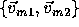 in the model which match two vectors in the scene
in the model which match two vectors in the scene 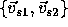 . There are several different transformations which superimpose the model set on the scene set (or vice versa).
. There are several different transformations which superimpose the model set on the scene set (or vice versa).


Figure 2, below, illustrates the basic problem. There are two matching point sets 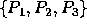 or, alternatively, a matching point
or, alternatively, a matching point 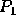 and two vectors
and two vectors 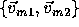 in the model which match two vectors in the scene
in the model which match two vectors in the scene 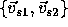 . There are several different transformations which superimpose the model set on the scene set (or vice versa).
. There are several different transformations which superimpose the model set on the scene set (or vice versa).

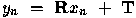 , the basic rotation matrix is
, the basic rotation matrix is


These can be combined to form

representing the point to be transformed as 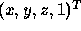 in homogeneous coordinates. If
in homogeneous coordinates. If 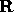 is a rotation matrix in 3D orthogonal space, then
is a rotation matrix in 3D orthogonal space, then  and the determinant of
and the determinant of 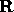 is 1. Representing
is 1. Representing 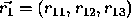 and so on this gives 6 constraint equations,
and so on this gives 6 constraint equations,
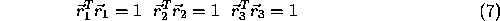

The first intuitive approach to define a rotation matrix might be the fixed axis method , e.g.
 to the origin
to the origin
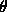 about the original x-axis (positive rotation is from y to z)
about the original x-axis (positive rotation is from y to z)
 about the original y-axis (positive rotation is from z to x)
about the original y-axis (positive rotation is from z to x)
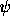 about the original z-axis (positive rotation is from x to y)
about the original z-axis (positive rotation is from x to y)
This leads to a rotation matrix formed by the concatenation of the matrices for the three single angle rotations about the fixed axes,
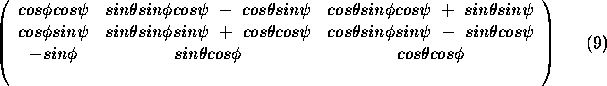
Note also that the angles can be recovered, 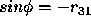 ,
, 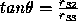 and
and 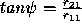 .
.
A second method to define a rotation matrix, illustrated in Figure 2, above, is based on a rotation about an
arbitrary axis, 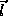 , by an angle
, by an angle  .
. 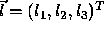 ,
,
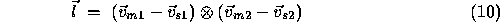
and  is defined
is defined
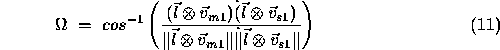
The rotation matrix is
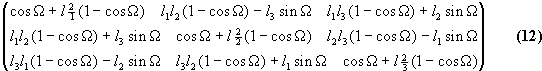
Re-arranging, we can also express  and
and 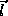 in terms of the rotation matrix elements.
in terms of the rotation matrix elements.
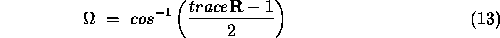
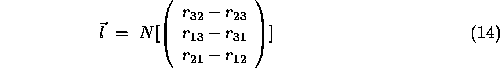
The trace of a square matrix  is defined as the sum of the diagonal elements,
is defined as the sum of the diagonal elements,  . N is a normalisation operator,
. N is a normalisation operator,  .
.



[ Pose Estimation: Contents |
Least squares estimation of 3D pose ]