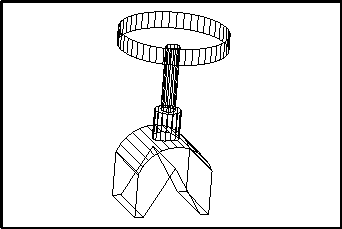
Figure 2: A solid model of an optical stand


The CSG ( Constructive Solid Geometry ) representation of an object is specified in terms of a set of 3D volumetric primitives, which include blocks, cylinders, cones, spheres etc., and a set of Boolean operators, for example union, intersection and difference. CSG descriptions of simple primitives are illustrated in Figure 1: Simple definition of CSG primitives and solids. In practice, the primitive descriptions can be much more complex, including for example ellipsoidal shapes or a more general quadric description termed a ``superquadric'', which consists of a second order surface with variable parameters. CSG representations define the object volume and the surface area of the object unambiguously, and require small amounts of storage to encode quite complex objects.
Primitive volumes may be derived in several ways, of which the most common is the swept volume. A shape is represented firstly by a two-dimensional template. A sweeping rule defines the motion of the 2D template through three-dimensional space. Figure 1 shows two examples of this, a linear extrusion of a circle to form a cylinder and a rotation of a triangle to form a cone. The trajectory of the sweeping rule may be more complex. Similarly the template may be fixed throughout the sweep, or vary in size. Figure 2, below, shows a full model of an optical stand which has been built from the union and difference of simple solid primitives, formed in turn by extrusion and rotation of 2D templates in 3D space.




[ Representing 3D solid objects |
Surface boundary representations ]
Comments to: Sarah Price at ICBL.