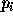 is the sum of the path cost between the starting pixel p1 and the current pixel
is the sum of the path cost between the starting pixel p1 and the current pixel 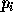 ,
, 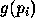 , and an estimate of the path cost from
, and an estimate of the path cost from 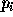 to the end pixel
to the end pixel 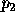 ,
, 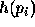 .
.


It is assumed that an edge detector, such as the Sobel or Canny operator, has been applied to an intensity image, although the processes described are equally applicable to 3D boundary data. Although not essential, it is easier to process data which has also been thresholded and thinned.
In many treatments, the objective is to create a continuous edge from a point p1 at ( x1 , y1 ) to another point p2 at ( x2 , y2 ) by finding the optimum path through the edge data. The basic principle is to form a graph from p1 to p2 in which the nodes represent the edge pixels and the arcs the one pixel steps between them in which each arc has an associated cost function. The cost function may be based on several criteria, but in general it is reasonable to install some function of the edge strength of the added pixel, the difference in edge direction between successive pixels and possibly to favour those pixels which are nearest to the direct line of sight to the final pixel, p2. Then the A* algorithm can be applied; the total cost function f( pi ) at 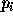 is the sum of the path cost between the starting pixel p1 and the current pixel
is the sum of the path cost between the starting pixel p1 and the current pixel 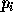 ,
, 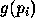 , and an estimate of the path cost from
, and an estimate of the path cost from 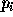 to the end pixel
to the end pixel 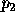 ,
, 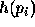 .
.
Expand the start node, n1 corresponding to p1 ; i.e. put all successor nodes on a list called OPEN. Evaluate the cost function of each expanded node. While (OPEN is not empty) and (no solution output) Remove the nodeof minimum cost function from OPEN. If
then output the solution by tracing nodes back to start node else expand node
by putting successors on OPEN and evaluate the cost function of each expanded node.
This approach is fine, but the common problem is that the end pixel is not known when you start to track the boundary. Indeed the start pixel is not generally known either. Hence a yet more heuristic strategy must be adopted. Considering Figure 1, below, we wish to track firstly in front of the edge, i.e. in the direction b,c, or e, and then behind the edge, i.e. in the direction d,f or g. A possible algorithm is
RepeatScan the image to find the strongest remaining edge point. Mark the edge as the initial and current contour point. Repeat Expand in front of the current contour point by adding the unmarked edge point with the minimum cost function (as above). Mark this latter point as the current point. Until (no more edge points are found) Mark the initial point as the current point Repeat Expand all unmarked edges behind the current contour point by adding the unmarked edge point with the minimum cost function (as above). Mark this latter point as the current point. Until (no more edge points are found) Save the list of marked edge points as a single contour Until (no more edge points are found)
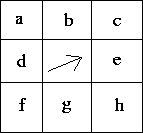
Figure 1: Bidirectional edge tracking




Comments to: Sarah Price at ICBL.
(Last update: 22th April, 1996)