 Piecewise Polynomials
Piecewise Polynomials
( Splines)

The 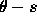 curve described above has the advantage that it can represent any
form of curve but it may not be particularly succinct, nor appropriate for matching purposes. The pure parametric form of boundary representation is succinct, but is limited in the boundaries it can describe. An intermediate representation is to use piecewise polynomials to represent a continuous boundary of arbitrary shape, in which perhaps one polynomial is used to represent each segment of the curve separated by peaks in
curve described above has the advantage that it can represent any
form of curve but it may not be particularly succinct, nor appropriate for matching purposes. The pure parametric form of boundary representation is succinct, but is limited in the boundaries it can describe. An intermediate representation is to use piecewise polynomials to represent a continuous boundary of arbitrary shape, in which perhaps one polynomial is used to represent each segment of the curve separated by peaks in 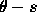 space. In general, the number of boundary segments we require is inversely related to the complexity of the segment description. For example we may use linear
space. In general, the number of boundary segments we require is inversely related to the complexity of the segment description. For example we may use linear

quadratic
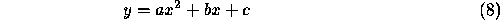
or cubic representations.
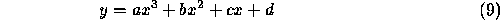
Cubic polynomials are, historically speaking, the original ``splines'' named after the flexible wooden or rubber templates used by draughtsmen to draw complex curves. The piecewise approximation technique may be applied to higher order polynomials in principle, but in a computer vision system this is rarely useful in view of the lack of accuracy of the segmented description derived from the image data.
A given boundary, consisting of a set of edge points, may be regression fitted to a polynomial function; in the straight line case, the best-fit
straight line is defined
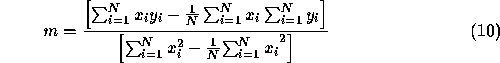

where 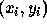 are the set of N boundary points, and c is the intercept
of the straight line of gradient m. The disadvantage of regression fitting is that the entire expression of equations 10 and 11 must be recalculated for each additional point. The technique is extensible to higher order curves although the expression is correspondingly more complex. Piecewise functions offer a direct way of achieving local control and simpler functional representations. For k sub-intervals,
are the set of N boundary points, and c is the intercept
of the straight line of gradient m. The disadvantage of regression fitting is that the entire expression of equations 10 and 11 must be recalculated for each additional point. The technique is extensible to higher order curves although the expression is correspondingly more complex. Piecewise functions offer a direct way of achieving local control and simpler functional representations. For k sub-intervals,
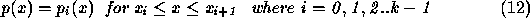
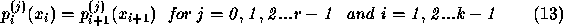
where 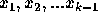 are the breakpoints,
are the breakpoints,
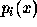 is the polynomial expression for the i'th segment,
is the polynomial expression for the i'th segment,
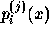 is the j'th derivative of
is the j'th derivative of 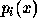 ,
and m is the degree of the polynomial.
Equation 13 expresses continuity constraints. Thus, if r=0 there are no constraints. If r=1 the function must be piecewise continuous, but there are no constraints on the derivatives. If r=2, the function must be piecewise continuous and the gradients must be
equal at the breakpoint and so on. If r=m+1 then the entire boundary is represented by a single polynomial, and
we are back to a simple parametric representation.
,
and m is the degree of the polynomial.
Equation 13 expresses continuity constraints. Thus, if r=0 there are no constraints. If r=1 the function must be piecewise continuous, but there are no constraints on the derivatives. If r=2, the function must be piecewise continuous and the gradients must be
equal at the breakpoint and so on. If r=m+1 then the entire boundary is represented by a single polynomial, and
we are back to a simple parametric representation.
Example -- Linear Polynomial (m=1, r=1)
In Figure 10, below, the boundary is represented by a series of linear segments
in the form

where
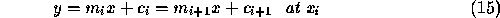
but
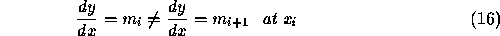
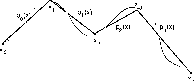
Figure 10: Approximation by linear segments
Example -- Quadratic Polynomial (m=2, r=2)
In Figure 11, the boundary is represented by segments of the form
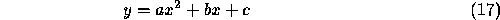
Since m=r, this is the maximum number of constraints which leads to a non-trivial solution. ( If r=m+1=3 in this case, then the piecewise functions, the first and the second derivatives would all be equal at each breakpoint which means the whole boundary is represented by a single quadratic).
For m=2, and r=2, the functions and first derivatives are equivalent at the breakpoint, 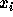 , but the second derivatives are not.
, but the second derivatives are not.
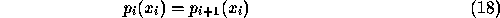

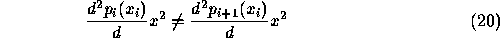

Figure 11: Approximation by arc segments
One way of determining the breakpoints is to differentiate the  curve previous to least squares fitting; peaks in the differential indicate points of high curvature which provide the necessary breakpoints. Alternatively, a running least squares fit can be used as discussed earlier in the section on edge tracking. As each new point is added the best fit is recomputed along with an error measure ( e.g. the of the perpendicular distance of the points from the line ). When this error measure exceeds a threshold value a new segment is started. Finally, a successive splitting and merging algorithm may be used. Given a curve, an algorithm for piecewise linear approximation between two endpoints is expressed recursively, commencing with Breakpoint
curve previous to least squares fitting; peaks in the differential indicate points of high curvature which provide the necessary breakpoints. Alternatively, a running least squares fit can be used as discussed earlier in the section on edge tracking. As each new point is added the best fit is recomputed along with an error measure ( e.g. the of the perpendicular distance of the points from the line ). When this error measure exceeds a threshold value a new segment is started. Finally, a successive splitting and merging algorithm may be used. Given a curve, an algorithm for piecewise linear approximation between two endpoints is expressed recursively, commencing with Breakpoint 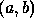 where a and b are the initial line extremities,
where a and b are the initial line extremities,
Procedure Breakpoint 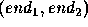 Draw a straight line between the two endpoints
Draw a straight line between the two endpoints 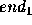 and
and 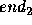 Set breakpoint = NULL
For every point on the line,
Compute perpendicular distance d to straight line
If d is above a threshold then record distance and point
Pick the furthest perpendicularly distanced point from the
current approximation to set new breakpoint, breakpoint
If (
Set breakpoint = NULL
For every point on the line,
Compute perpendicular distance d to straight line
If d is above a threshold then record distance and point
Pick the furthest perpendicularly distanced point from the
current approximation to set new breakpoint, breakpoint
If (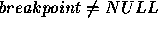 ) then
Breakpoint(
) then
Breakpoint(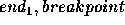 )
Breakpoint(
)
Breakpoint(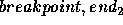 )
)
 [ Grouping Edges: Contents ]
[ Grouping Edges: Contents ]

Comments to: Sarah Price at ICBL.
(Last update: 22th April, 1996)
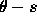 curve described above has the advantage that it can represent any
form of curve but it may not be particularly succinct, nor appropriate for matching purposes. The pure parametric form of boundary representation is succinct, but is limited in the boundaries it can describe. An intermediate representation is to use piecewise polynomials to represent a continuous boundary of arbitrary shape, in which perhaps one polynomial is used to represent each segment of the curve separated by peaks in
curve described above has the advantage that it can represent any
form of curve but it may not be particularly succinct, nor appropriate for matching purposes. The pure parametric form of boundary representation is succinct, but is limited in the boundaries it can describe. An intermediate representation is to use piecewise polynomials to represent a continuous boundary of arbitrary shape, in which perhaps one polynomial is used to represent each segment of the curve separated by peaks in 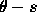 space. In general, the number of boundary segments we require is inversely related to the complexity of the segment description. For example we may use linear
space. In general, the number of boundary segments we require is inversely related to the complexity of the segment description. For example we may use linear 


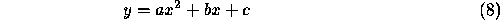
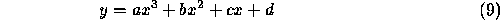
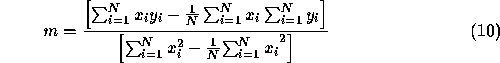

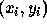 are the set of N boundary points, and c is the intercept
of the straight line of gradient m. The disadvantage of regression fitting is that the entire expression of equations 10 and 11 must be recalculated for each additional point. The technique is extensible to higher order curves although the expression is correspondingly more complex. Piecewise functions offer a direct way of achieving local control and simpler functional representations. For k sub-intervals,
are the set of N boundary points, and c is the intercept
of the straight line of gradient m. The disadvantage of regression fitting is that the entire expression of equations 10 and 11 must be recalculated for each additional point. The technique is extensible to higher order curves although the expression is correspondingly more complex. Piecewise functions offer a direct way of achieving local control and simpler functional representations. For k sub-intervals,
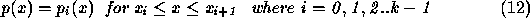
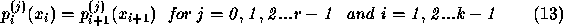
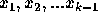 are the breakpoints,
are the breakpoints,
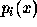 is the polynomial expression for the i'th segment,
is the polynomial expression for the i'th segment,
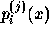 is the j'th derivative of
is the j'th derivative of 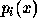 ,
and m is the degree of the polynomial.
Equation 13 expresses continuity constraints. Thus, if r=0 there are no constraints. If r=1 the function must be piecewise continuous, but there are no constraints on the derivatives. If r=2, the function must be piecewise continuous and the gradients must be
equal at the breakpoint and so on. If r=m+1 then the entire boundary is represented by a single polynomial, and
we are back to a simple parametric representation.
,
and m is the degree of the polynomial.
Equation 13 expresses continuity constraints. Thus, if r=0 there are no constraints. If r=1 the function must be piecewise continuous, but there are no constraints on the derivatives. If r=2, the function must be piecewise continuous and the gradients must be
equal at the breakpoint and so on. If r=m+1 then the entire boundary is represented by a single polynomial, and
we are back to a simple parametric representation.

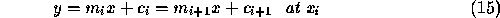
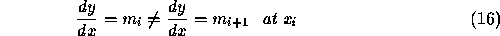

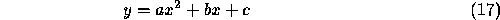
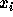 , but the second derivatives are not.
, but the second derivatives are not.
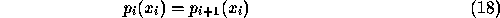

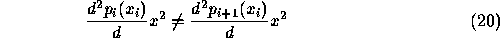

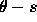 curve previous to least squares fitting; peaks in the differential indicate points of high curvature which provide the necessary breakpoints. Alternatively, a running least squares fit can be used as discussed earlier in the section on edge tracking. As each new point is added the best fit is recomputed along with an error measure ( e.g. the of the perpendicular distance of the points from the line ). When this error measure exceeds a threshold value a new segment is started. Finally, a successive splitting and merging algorithm may be used. Given a curve, an algorithm for piecewise linear approximation between two endpoints is expressed recursively, commencing with Breakpoint
curve previous to least squares fitting; peaks in the differential indicate points of high curvature which provide the necessary breakpoints. Alternatively, a running least squares fit can be used as discussed earlier in the section on edge tracking. As each new point is added the best fit is recomputed along with an error measure ( e.g. the of the perpendicular distance of the points from the line ). When this error measure exceeds a threshold value a new segment is started. Finally, a successive splitting and merging algorithm may be used. Given a curve, an algorithm for piecewise linear approximation between two endpoints is expressed recursively, commencing with Breakpoint 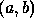 where a and b are the initial line extremities,
where a and b are the initial line extremities,
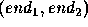 Draw a straight line between the two endpoints
Draw a straight line between the two endpoints 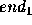 and
and 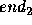 Set breakpoint = NULL
For every point on the line,
Compute perpendicular distance d to straight line
If d is above a threshold then record distance and point
Pick the furthest perpendicularly distanced point from the
current approximation to set new breakpoint, breakpoint
If (
Set breakpoint = NULL
For every point on the line,
Compute perpendicular distance d to straight line
If d is above a threshold then record distance and point
Pick the furthest perpendicularly distanced point from the
current approximation to set new breakpoint, breakpoint
If (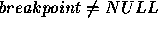 ) then
Breakpoint(
) then
Breakpoint(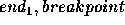 )
Breakpoint(
)
Breakpoint(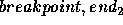 )
)
 [ Grouping Edges: Contents ]
[ Grouping Edges: Contents ]
