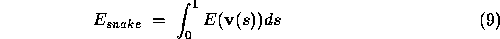
The model of the contour is defined to lie where the energy function of Equation 1 is a minimum.

Using variational calculus, the Euler-Lagrange condition shows that the minimum energy 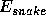is obtained when,

where 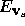is the partial derivative of the energy, E with respect to , and 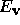is the partial derivative of E with respect to 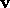. Using Equation 2 to define the internal spline energy term, and denoting the external spline energy 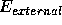, or 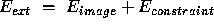, then Equation 10, above, becomes

To solve this equation, we assume that an initial estimate of the solution is available at time t=0, say. An evolution equation is formed.

From Equations 11 and 12 we note that a solution is found where 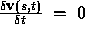, i.e. when the contour does not change shape as a function of evolving time. Solution of this equation is not trivial. First, numerous heuristic parameters must be assigned, including the weighting factors of the energy terms, and the number of iterations or time-steps of the algorithm. Second, the Euler-Lagrange equation is numerically unstable. This has led to a number of optional ``fixes'' discussed in the literature.