
Next: References
Here we briefly discuss least-squares fitting of spheres, cylinders,
cones and tori. Least-squares fitting of
surfaces other planes, even of simple geometric type, has been little studied;
for fitting of general algebraic curves and surfaces, see Taubin [8].
Linear least-squares fitting of second order curves and surfaces has been
considered
by several authors [2,3,7,6].
However, linear methods still do not exist to specifically produce right
cylinders and
cones---the reason is that the equations expressing the conditions for a
quadric to be a
right cylinder or a cone are not quadratic.
Instead typically, the problem is made linear by using the value of the
implicit quadratic form as a `pseudo-distance' from the surface to
approximate the true geometric distance. Such methods may be used to find
general
algebraic second order surfaces, but the solutions found are not
constrained to be right
cylinders or cones, and may be very different from the optimum surfaces of such
type.
For spheres, straightforward
algebraic methods work: under a suitable side constraint the
minimised algebraic distance equates to the geometric distance [6]; the
constraint must be chosen carefully, however.
Nonlinear methods which take into account the true geometric distance are
much more
reliable, assuming an initial approximate fit for the surface is known.
Such an initial
approximation can be found by estimating parameters such as axis of
revolution, curvatures,
etc from differential geometric quantities computed locally for small clusters
of points in the data set, or using approaches based on line
geometry [5].
Earlier nonlinear estimation approaches usually worked with cylinders and
spheres.
As a rule the equations contain positional parameters of centres or axes
and so they
become ill-conditioned in limiting situations, (for example, as the radius
of the cylinder
increases and it tends to a plane---see e.g. [1]). This is generally
unacceptable. We have devised nonlinear methods which are carefully
designed to overcome
this problem. We do this by making a faithful approximation
to the true distance function: this is one which is zero at the surface,
and also has the
correct value of the derivative there too. The main trick of our
approximation is to
replace a dependence on 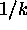 in the distance function (where k is a
surface curvature)
by a dependence on k in our approximation, thus avoiding problems as k
tends to zero.
In such cases, our method naturally returns a surface of lower order or
simpler type, and
we avoid singularities in the method.
in the distance function (where k is a
surface curvature)
by a dependence on k in our approximation, thus avoiding problems as k
tends to zero.
In such cases, our method naturally returns a surface of lower order or
simpler type, and
we avoid singularities in the method.
Full details may be obtained in our paper from
ftp://ralph.cs.cf.ac.uk/pub/papers/Geometry/fit.ps.


Next: References
Bob Fisher
Tue Oct 27 15:43:59 GMT 1998
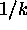 in the distance function (where k is a
surface curvature)
by a dependence on k in our approximation, thus avoiding problems as k
tends to zero.
In such cases, our method naturally returns a surface of lower order or
simpler type, and
we avoid singularities in the method.
in the distance function (where k is a
surface curvature)
by a dependence on k in our approximation, thus avoiding problems as k
tends to zero.
In such cases, our method naturally returns a surface of lower order or
simpler type, and
we avoid singularities in the method.