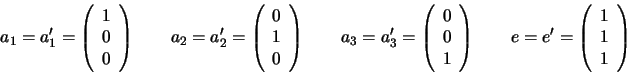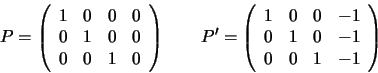


Next: Affine Reconstruction
Up: 3D Reconstruction from Multiple
Previous: 3D Reconstruction from Multiple
Simple parameter counting shows that we have 2nm independent
measurements and only
11 m + 3 n unknowns, so with enough points and
images the problem ought to be soluble. However, the solution can
never be unique as we always have the freedom to change the 3D
coordinate system we use. In fact, in homogeneous coordinates the
equations become
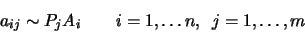 |
(5.4) |
So we always have the freedom to apply a nonsingular  transformation H to both projections
transformation H to both projections
 and world
points
and world
points
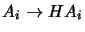 .
Hence, without further constraints,
reconstruction is only ever possible up to an unknown projective
deformation of the 3D world. However, modulo this fundamental
ambiguity, the solution is in general unique.
.
Hence, without further constraints,
reconstruction is only ever possible up to an unknown projective
deformation of the 3D world. However, modulo this fundamental
ambiguity, the solution is in general unique.
One simple way to obtain the solution is to work in a projective basis
tied to the 3D points [3]. Five of the visible points
(no four of them coplanar) can be selected for this purpose.
Exercise 5.1
:
Given the epipolar geometry, show how we can decide whether four
points are coplanar or not, by just considering their images in a
stereo pair. Hint: consider the intersection of a pair of image
lines, each linking two of the four points.
An alternative to this is to select the projection center of the first
camera as the coordinate origin, the projection center of the second
camera as the unit point, and complete the basis with three other
visible 3D points
A1, A2, A3 such that no four of the five
points are coplanar.
Exercise 5.2
:
Design an image-based test to check whether three points are coplanar
with the center of projection. Derive a test that checks that two
points are not coplanar with the base line of a stereo pair, assuming
that the epipolar geometry is known. Deduce a straightforward test to
check that the above five points form a valid 3D projective basis.
Let
a1, a2, a3 and
a'1, a'2, a'3 respectively be
the projections in image 1 and image 2 of the 3D points
A1, A2,
A3. Make a projective transformation of each image so that these
three points and the epipoles become a standard basis:
Also fix the 3D coordinates of
A1, A2, A3 to be respectively
It follows that the two projection matrices can be written:
Exercise 5.3
:
Show that the projections have these forms. (NB: Given only the
projections of
A1,A2,A3, each row of P,P' could have a
different scale factor since point projections are only defined up to
scale. It is the projections of the epipoles that fix these scale
factors to be equal).
Since the projection matrices are now known, 3D reconstruction is
relatively straightforward. This is just a simple, tutorial example so
we will not bother to work out the details. In any case, for precise
results, a least squares fit has to be obtained starting from this
initial algebraic solution (e.g. by bundle adjustment).



Next: Affine Reconstruction
Up: 3D Reconstruction from Multiple
Previous: 3D Reconstruction from Multiple
Bill Triggs
1998-11-13