Gérard Medioni
Institute for Robotics and Intelligent Systems
Integrated Media Systems Center
University of Southern California
Over the past several years, we have developed a methodology for tackling early vision problems in 2-D, 3-D, and more recently N-D. The inputs are tokens in the form of points, edge or surface elements, or any combination of these. The formalism, as described below, is founded on two components: tensor calculus for representation, and non-linear voting for data communication. The proposed method is non-iterative, requires no initial guess or thresholding, and the only free parameter is scale. It can handle the presence of multiple structures even in extreme noise corruption, while still preserving discontinuities.
This research addresses the ubiquitous problem of structure inference from sparse data. We developed a unified computational framework, which properly implements the smoothness constraint to generate descriptions in terms of surfaces, regions, curves, and labeled junctions, from sparse, noisy, binary data in 2-D or 3-D. Each input site can be a point, a point with an associated tangent direction, a point with an associated normal direction, or any combination of the above. Each input site communicates its information, a tensor, to its neighborhood through a predefined tensor field, and casts a tensor vote. Each site collects all the votes cast at its location and encodes them into a new tensor. A local, parallel marching process then simultaneously detects features. The described approach is very different from traditional variational approaches, as it is non-iterative. Furthermore, the only free parameter is the size of the neighborhood, related to the scale.
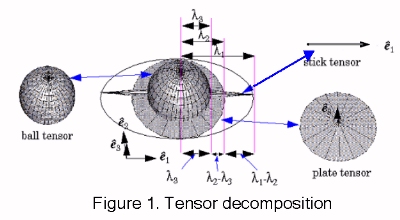
To capture first order differential geometry information and its singularities, a second order symmetric tensor is used. It captures both the orientation information and its confidence, or saliency. Such a tensor can be visualized as an ellipse in 2-D, or an ellipsoid in 3-D. Intuitively, the shape of the tensor defines the type of information captured (point, curve, or surface element), and its size represents the saliency. By perceptual saliency we mean the perceived importance of structures such as surfaces, curves, junctions and regions. For instance, in 2-D, a very salient curve element is represented by a thin ellipse, whose major axis represents the estimated tangent direction, and whose length reflects the saliency of the estimation. In 3-D, a point on a smooth surface is represented by a tensor in the shape of an elongated ellipsoid (stick tensor) with its major axis along the surface normal. A junction of two surfaces (a curve) is represented by a tensor in the shape of a circular disk (plate tensor) which is perpendicular to the curve's tangent. Alternatively, the plate can be thought of as spanning the 2-D subspace defined by the two surface normals, in the case of the surface junction. Finally, an isolated point or a junction of curves has no orientation preference and is represented by a tensor in the shape of a sphere (ball tensor).

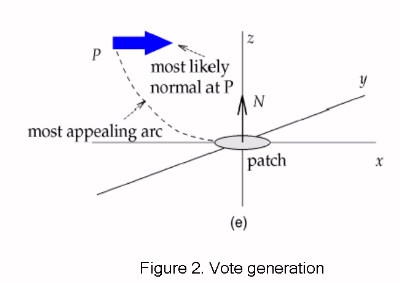
Each token is first decomposed into the basis tensors, and then broadcasts its information. A voting field for each basic component is used to look up the orientation and magnitude of the votes cast. All voting fields are based on the fundamental 2-D stick voting kernel. As seen in Fig. 2 the orientation of the stick vote is normal to the smoothest circular path connecting the voter and receiver that is perpendicular to the normal (the stick) at the voter's location. The magnitude of the vote decays with distance and curvature according to the following equation:
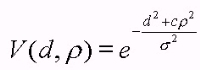
Vote accumulation is performed by tensor addition or equivalently by addition of 3x3 matrices (in the 3-D case), therefore it is computationally inexpensive. After voting has been completed, we can compute the eigensystem of the resulting tensor which encapsulates all the information propagated to the location. The stick component, which is parallel to the eigenvector corresponding to the largest eigenvalue and its magnitude (saliency) is equal to the difference of the largest and the second largest eigenvalue, encodes the likelihood of the point belonging to a smooth surface. The plate component spanned by the eigenvectors corresponding to the two largest eigenvalues and whose saliency is the difference of the second and third eigenvalue encodes the likelihood that the point belongs to a smooth curve or a surface junction. Finally, the ball component that has no preference of orientation and its saliency is equal to the smallest eigenvalue encodes the likelihood of the point being a junction. Assuming that noisy points are not organized in salient perceptual structures they can easily be identified by their low saliency.
Structures can be extracted after a dense tensor vote has been performed. The difference is that in this case votes are also collected at previously unoccupied locations and surface, curve and junction saliency maps are filled in. Surfaces and curves are extracted as the local maxima of surface and curve saliency respectively, while junctions can be extracted as the local maxima of junction saliency without any form of propagation. Since calculating votes for every location in the volume containing the data points is pointless and impractical, surface and curve extraction begins from seeds, location with highest saliency, and voting is performed only towards the directions indicated by the surface normals and curve tangents.
The basic framework has been extended to incorporate curvature information [15, 18], while a first order tensor voting scheme, which can detect region boundaries, bounding curves or surfaces and endpoints of curves, has been implemented with promising results [19].
The generalization to N dimensions is straightforward by converting the 2- or 3-D tensors to N-D ones which correspond to hyper-ellipsoids. The fundamental stick voting kernel can easily be obtained in N-D by the use of symmetry and the other fields can be derived by integration. In order to detect a geometric variety of dimension N-1, surface-ness becomes hyper-surface-ness, defined locally by a stick tensor normal to the hyper-surface that is encoded by the eigenvector corresponding to the largest eigenvalue. Similarly, junction-ness is represented by a hyper-sphere where all eigenvalues are equal and there is perfect uncertainty of orientation. Salient structures can still be detected as local maxima of the corresponding saliency map. Results of N-D Tensor Voting have been published in [14, 17, 20].
Another challenging issue is the need for multiple scales. As the sole free parameter in our current framework, scale indeed plays a significant role in determining the quality of our inference results. The drawback of our current implementation is that a single scale of the voting function is applied to the entire data set. This lack of versatility can cause problems in case of uneven data distribution. A small scale is optimal for dense, noise-free regions with fine details, if the desired output is an accurate description in terms of perceptual structure. This small scale, though, would be inadequate to establish satisfactory information propagation in sparser regions of the data set. The current solution, a trade-off between unwanted smoothing in dense areas and weak enforcement of continuity in sparse areas, is clearly not ideal. We are investigating ways to make multi-scale voting an integral part of our new tensor voting framework. Fine structures can be detected using a small scale initially. At the next stages, larger scales will be used to propagate information in larger regions and bridge gaps. This scheme is capable of preserving details where they exist, facilitating adequate information propagation in sparse areas, and grouping compatible structures extracted at previous stages.
Students currently working on Tensor Voting:
Journal and Conference Papers:
Updated 03/20/2002
by Philippos Mordohai