Next: Self-calibration Up: Computer Vision IT412 Previous: Calculating the fundamental matrix

What information can be extracted from two scenes?

In 1996, Faugeras and Robert [3] completely solved the problem about what could be predicted about a third view of an object, given two other views. This problem is central to stereo, motion, and object recognition. They describe the geometry of three cameras, illustrated in figure 5, as follows:

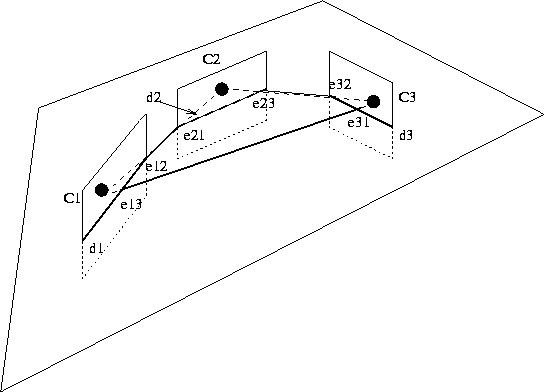
**Figure:** The geometry of three camera systems. There are three optical centres, six epipoles, and three particular epipolar lines.
$\begin{figure} \par \centerline{ \psfig {figure=figure5.ps,width=12cm} } \par\end{figure}$

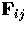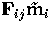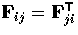Denoting the cameras by 1, 2 and 3, there are now three fundamental matrices ${\bf F}_{ij}$ , with the obvious convention on the indices. If m_i is a pixel in image i, its epipolar line in image j is represented by ${\bf F}_{ij}\tilde{\bf m}_i$ . Note that we have ${\bf F}_{ij} = {\bf F}_{ji}^{\top}$ . The plane containing the three optical centres is called the trifocal plane. It intersects each image plane along a line d_i which contains the epipoles e_ii+1 and e_ii+2 of camera i with respect to cameras i+1 and i+2 (all mod 3). Because of the epipolar geometry, we have

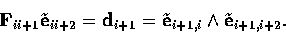
$\begin{displaymath} {\bf F}_{ii+1}\tilde{\bf e}_{ii+2} = {\bf d}_{i+1} = \tilde{\bf e}_{i+1,i} \wedge \tilde{\bf e}_{i+1,i+2}. \end{displaymath}$

In this work it is assumed that the three fundamental matrices are known, but not that the system is fully calibrated. It is shown that it is possible to predict how a scene would look from a third viewpoint, given two other views. They consider predicting the third view of points, lines, and curvatures.

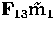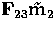The prediction of points is very simple. We assume that we have two corresponding pixels m₁ and m₂ in images 1 and 2. Them m₃ must belong to the epipolar line of m₁ in the third image, given by ${\bf F}_{13}\tilde{\bf m}_1$ , and to the epipolar line of pixel m₂ in the third image, given by ${\bf F}_{23}\tilde{\bf m}_2$ .Therefore, m₃ belongs to the intersection of these two lines, and we can write

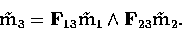
$\begin{displaymath} \tilde{\bf m}_3 = {\bf F}_{13}\tilde{\bf m}_1 \wedge {\bf F}_{23}\tilde{\bf m}_2. \end{displaymath}$

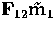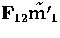The prediction of lines is also simple. We assume now that we are given two corresponding lines l₁ and l₂ in images 1 and 2. The problem is to determine the position of l₃ in image 3. Let m₁, m'₁ be two points of l₁. They define two points m₂, m'₂ of l₂ as the intersections of the epipolar line of m₁ represented by ${\bf F}_{12}\tilde{\bf m}_1$ and of m'₁ represented by ${\bf F}_{12}\tilde{\bf m'}_1$ with l₂. Therefore we can write

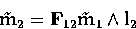
$\begin{displaymath} \tilde{\bf m}_2 = {\bf F}_{12}\tilde{\bf m}_1 \wedge {\bf l}_2 \end{displaymath}$

and

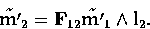
$\begin{displaymath} \tilde{\bf m'}_2 = {\bf F}_{12}\tilde{\bf m'}_1 \wedge {\bf l}_2. \end{displaymath}$

Therefore, the line l₃ is defined by the two points m₃ and m'₃, intersections of the epipolar lines of m₁ and m'₁ and m₂ and m'₂ in the third image. Therefore we can write

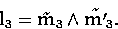
$\begin{displaymath} {\bf l}_3 = \tilde{\bf m}_3 \wedge \tilde{\bf m'}_3. \end{displaymath}$

The prediction of curvatures is slightly more complicated and will not be covered in these lectures.

Next: Self-calibration Up: Computer Vision IT412 Previous: Calculating the fundamental matrix

Robyn Owens
10/29/1997