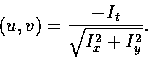

Next: Structure from motion
Up: Computer Vision IT412
Previous: The motion field
Optical flow is the apparent motion of brightness patterns in the
image. Generally, optical flow corresponds to the motion field, but
not always. For example, the motion field and optical flow
of a rotating barber's pole
are different, as illustrated in figure 3. In general, such cases
are unusual, and for this lecture we will assume that optical flow
corresponds to the motion field.
Figure:
The motion field and optical flow of a barber's pole.
 |
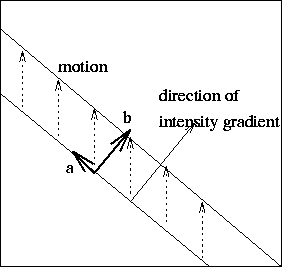
One problem we do have to worry about, however, is that we are only able to
measure the component of optical flow that is in the direction of the
intensity gradient. We are unable to measure the component tangential
to the intensity gradient. This problem is illustrated in figure 4, and further
developed below.
Figure:
The aperture problem. We can only measure the component b.
 |
Denote the intensity by I(x,y,t). This is a function of three variables
as we now have spatiotemporal variation in our signal. To see how
I changes in time, we differentiate with respect to t:
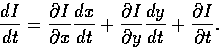
Now, we assume that the image intensity of each visible scene point is
unchanging over time (for example, shadows and illuminations are
not changing due to any motion), so we have
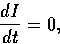
which implies
Ixu + Iyv + It = 0,
where the partial derivatives of I are denoted by subscripts, and u and
v are the x and y components of the optical flow vector.
This last equation is called the optical flow constraint equation
since it expresses a constraint on the components u and v of the optical
flow.
The optical flow constraint equation can be rewritten as
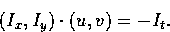
Thus, the component of the image velocity in the direction of the
image intensity gradient at the image of a scene point is
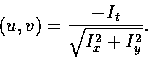
We cannot, however, determine the component of the optical flow at
right angles to this direction. This ambiguity is known as the
aperture problem.
There are two main approaches to reconstructing three dimensional motion from
motion in the image plane:
- Convert the motion problem to a stereo problem and find the
correspondence between a number of points in the image at time t
to the image at time
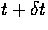 .
. - Computer the optical flow and use its geometrical properties
to deduce three dimensional information about the scene and the
motion.


Next: Structure from motion
Up: Computer Vision IT412
Previous: The motion field
Robyn Owens
10/29/1997
![]()
![]()
![]()