Feature detection via phase congruency

Rather than assuming that what an image should be compressed into is a set of edges, the phase congruency model of feature detection assumes that the compressed image format should be high in information (or entropy), and low in redundancy. Thus, instead of searching for points where there are sharp changes in intensity, this model searches for patterns of order in the phase component of the Fourier transform. Phase is chosen because the experiments of Oppenheim and Lim [9] demonstrated that it is crucial to the perception of visual features. Further physiological evidence [6] indicates that the human visual system responds strongly to points in an image where the phase information is highly ordered. Thus the phase congruency model defines features as points in an image with high phase order.

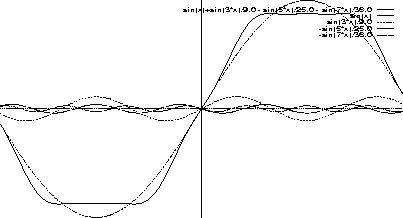
The phase congruency model is a frequency-based model of visual processing. It supposes that, instead of processing visual data spatially, the visual system is capable of performing calculations using the phase and amplitude of the individual frequency components in a signal. Thus, the underlying computational tool is the Fourier transform, or one of its equivalents. To this end, let us suppose that we can represent our image signal in the Fourier domain. To simplify the presentation, we will assume a simple one-dimensional signal, representing a 1D slice through an image. Such a signal, say f(x), is reconstructed from its Fourier transform by

$$f(x) = \int_{- \infty}^{\infty} a_{\omega} \cos(T \omega x + \phi_{\omega})d \omega,$$

where, for each frequency $\omega$, $a_{\omega}$ is the amplitude of the cosine wave and $T \omega x + \phi_{\omega}$ is the phase offset of that wave. The term T is related to the size of the image window, and from now on we will assume it is 1.

For example, if the image signal were a simple step edge, then

$$f(x) = \frac{-4}{\pi} \int_{- \infty}^{\infty} \frac{1}{2\omega + 1} \cos(\omega x + \pi/2)d \omega,$$

and, at the point of the step edge (x = 0), all the phase terms are aligned at $\pi/2$. This is the only place in the signal where there is congruency in the phase values; at all other points, the phase values of individual frequency components assume differing values between 0 and $2 \pi$.

 

Figure 1: All the Fourier terms for a periodic step edge are in phase at each step point.

 

Figure 2: All the Fourier terms for a periodic bar feature are in phase at each peak and trough.

 

Figure 3: All the Fourier terms for a periodic trapezoid wave form have maximal congruency at the point of tangent discontinuity where the Mach bands are seen.

A similar congruency of phase values occurs if the image signal is a triangular waveform, representing a tangent discontinuity and, in general, points in any signal where there is local maximal congruency or order in the phase values are precisely those points where humans perceive features [6]. That is, if a human were asked to draw a sketch of the image, localising precisely the edges or markings of interest as seen in the scene, then the points chosen would be those were there is maximal order in the phase components of a frequency-based representation of the signal.

We need to make precise what it is we mean by phase congruency. This is done by defining the phase congruency function, PC(x), at each point x in the signal. We have

$$PC(x) = \max_{\theta \in [0, 2\pi)} \frac{\int a_{\omega} \c... ...x + \phi_{\omega} - \theta)d \omega}{\int a_{\omega}d \omega}.$$

To understand this definition, we can think of our signal f(x), at any point x in the image, as being made up of the sum of various sine waves at different amplitudes and phase angles, which we plot on a vector map.

 

Figure 4: The individual vectors making up the signal.

If we find the mean phase angle and then calculate the standard deviation of all these phase angles about this mean we will have a measure of phase congruency, but not a good one, since such a measure gives a large deviation of 355^o from 1^o, when in fact it is small. To overcome this problem, the phase congruency function PC needs to be defined as above, where the cosine term captures the proximity of 355^o to 1^o. The $\theta$ that maximizes this expression for PC represents the weighted mean phase angle and since, by Taylor's theorem, we have $\cos(x) \approx 1 - \frac{x^2}{2}$for small x, we see that PC is a measure of the variance is the phase values of the signal. When PC is equal to 1, the phase terms are all equal, as is the case at the discontinuity in a step function. Otherwise, PC takes on some value between 0 and 1.

Although the definition of PC captures precisely what it is we want to measure, it is an awkward function to implement. Luckily, some simple trigonometric manipulations suffice to prove that PC is proportional to a well-known computation in biological vision, namely the local energy in a signal.

The local energy of a signal is defined in terms of the signal and its Hilbert transform. The Hilbert transform has a somewhat complicated definition in the spatial domain, namely

$$h(x) = \int_{-\infty}^{\infty} \frac{f(y)}{x-y}dy.$$

But this corresponds to simple phase shifting in the frequency domain. Specifically, the positive frequency terms are phase shifted by 90^o and the negative frequency terms are phase shifted by -90^o; the zero frequency, or d.c. term, is set to zero, since phase shifting has no meaning here. Thus, in the frequency domain,

$${\cal F}(h)(\omega) = i \mbox{sgn}(\omega){\cal F}(f)(\omega),$$

where sgn is the function that returns the sign of its argument. Thus, if

$$f(x) = \int_{- \infty}^{\infty} a_{\omega} \cos(\omega x + \phi_{\omega})d \omega,$$

then

$$h(x) = - \int_{- \infty}^{\infty} a_{\omega} \sin(\omega x + \phi_{\omega})d \omega.$$

We can define a vector E at a point x by

$${\bf E}(x) = f(x){\hat {\bf i}} + h(x){\hat {\bf j}},$$

where ${\hat {\bf i}}$ and ${\hat {\bf j}}$ are the unit vectors along the x and y axes. At any particular point x in the signal, E is the vector sum (or integral) of the Fourier terms. The nth component is a vector of length a_n making an angle of $nx + \phi_n$with the x axis.

The magnitude of the vector E is called the local energy of the signal (sometimes also called the envelope of the signal) and it is defined as

$$\Vert {\bf E} \Vert = \sqrt{f(x)^2 + h(x)^2}.$$

Local peaks in the local energy function correspond to local peaks in the phase congruency function.

The argument

$$Arg(x) = \mbox{atan2} (\frac{h(x)}{f(x)})$$

gives the angle at which the phase congruency occurs, and can be used to define the feature type.

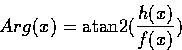
As was mentioned earlier, the human visual system has the capacity to simulate convolution by odd and even symmetric filters in quadrature. That the filters are in quadrature means not only that they form an odd and even symmetric pair (that is, the output of convolution by one filter is a 90^o phase shift of the output of the other), but also that they both have a zero mean value and the same sum-of-squares value. More specifically, if M_e represents the even filter and M_o represents the odd filter, then

$$\int M_e(x)dx = \int M_o(x)dx = 0,$$

and

$$\int M_e^2(x)dx = \int M_o^2(x)dx.$$

Moreover, the human visual system has the capacity to compute the sum of squares of the output from convolution with the odd and even symmetric filters, that is, by combining the output of the simple and complex cell responses, it computes a local energy for the signal. This is made more precise by defining

$$E(x) = \Vert {\bf E} \Vert = \sqrt{{(M_e * f(x)})^2 + {(M_o * f(x))}^2}.$$

The filters M_e and M_o need to be carefully designed. The even symmetric filter is chosen so that it covers as much of the frequency spectrum as possible, whilst eliminating the d.c. term. The odd symmetric filter is then just a 90^o phase shift filter of the even filter. Thus

$$M_e * f(x) \approx \int_{- \infty}^{\infty} a_{\omega} \cos(\omega x + \phi_{\omega})d \omega$$

and

$$M_o * f(x) \approx - \int_{- \infty}^{\infty} a_{\omega} \sin(\omega x + \phi_{\omega})d \omega.$$

It is now simple to see why $PC \propto E$, for

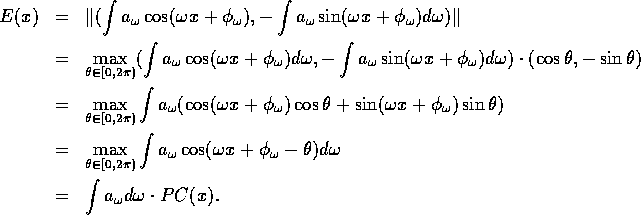
So, in order to search for local maxima in the phase congruency function, one equivalently searches for local maxima in the local energy function. These local maxima will occur at step edges of either parity (up or down), lines and bar edges, and other types of features such as the illusory Mach bands [8].

To illustrate how this works, figure 5 shows a simple test image that contains a variety of features at different contrasts. Figure 6 shows the output of a simple gradient-based edge detector (here, the Sobel operator). Note that the output depends on the relative contrast of the edge, and that the output for line features is two edges, one on either side of the line. Figure 7 shows the output of the local energy (or phase congruency) detector. Here we note that the output is a uniform response, regardless of the type or contrasts of the feature involved.

 

Figure 5: A simple test image.

 

Figure 6: The output of the Sobel operator.

 

Figure 7: The phase congruency map of the test image.

Local energy makes no assumptions about the shape of the features it is trying to detect, as it is only looking for points of local maximum phase congruency. Note that all other spatial edge detection methods have to make assumptions about the shape of the feature to be detected. Perona and Malik [10] have noted that most features in real images are composed of combinations of steps, roofs and ramps profiles, and that no linear feature detection scheme can detect such combinations. However, they prove that a quadratic scheme, such as the local energy scheme, is sufficient for the detection of all such features.

Figures 8 and 9 illustrate the local energy map and the detected features for the mandrill image.

 

Figure 8: The phase congruency map of the mandrill image.

 

Figure 9: The features after non-maxima suppression and thresholding.