Let us consider a different quadratic constraint that corresponds to the well known quadratic algebraic invariant of a conic
This constraint was first introduced in [3] and it was
shown to yield always elliptical solutions; the brief justification
given was that because of the immateriality of the scale of 
,
the inequality (4) can, w.l.o.g., turned into
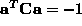and hence the minimisation (2) subject
to the constraint (4) can again be formulated like
in (3).
In the following, we give theoretical account of the method by demonstrating its key feature of ellipse specificity, i.e. that it gives always one and only one elliptical solution. But before that, we need to state two Lemmas that will naturally lead to an uniqueness theorem.
Let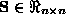 
and 
be symmetric matrices, with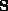 
positive definite. Let us define the spectrum 
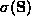as
the set of eigenvalues of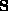 
and let 
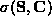analogously be the set of generalised eigenvalues
of (5).
Proof: Let the inertia 
be defined as the set
of signs of 
, and let 
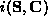analogously be the
inertia of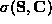 
. Then, the lemma is equivalent to
proving that 
.
As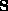 
is positive definite, it may be decomposed as 
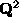for
symmetric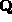 
, allowing us to write (5) as
.
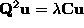Now, substituting 
and pre-multiplying by 
gives
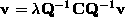so that 
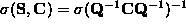and
thus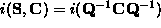 
.
From Sylvester's Law of Inertia [12] we have that for any
symmetric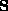 
and nonsingular 
,
.
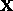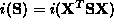Therefore, substituting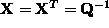 
we have 
. 
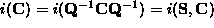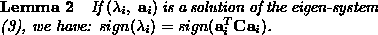
Proof: By pre-multiplying by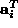 
both sides of
(3) we have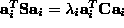 
. Since 
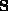is positive-definite, 
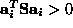and therefore 
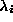and the scalar 
must have the same sign. 
Now we can state the following uniqueness theorem:
Proof: Since the non-zero eigenvalues of 
are
, from Lemma 1 we have that
has one and only one negative eigenvalue
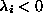, associated with a solution 
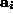; then, by applying
Lemma 2, the constraint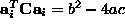 
is negative and
therefore 
is a set of coefficients representing an ellipse.
The constraint (4) is a conic invariant to
Euclidean transformations and so is the solution (see [1])
Theorem 1 does not state anything about the quality of the
unique elliptical solution, since classical optimisation theory states
that it might not be the global minimum of (2) under our
non-positive definite inequality constraint.
However, the physical solution (the actual ellipse) does not change
under linear scaling of the coefficients and therefore it can be
easily shown that the minimisation with the inequality constraint
(4) can be equivalently turned to a minimisation
with an equality constraint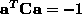 
.
By doing so, as illustrated in [2], we can say that:
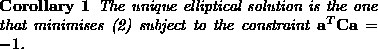
A more practical interpretation of this corollary is that the unique
elliptical solution is a local minimiser of the Rayleigh
quotient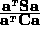 
and thus the
solution can also be seen as the best least squares ellipse under
a re-normalisation of the coefficients by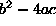 
. Although
experimental evidence would suggest that this statement could be
valid, a formal demonstration is currently not known to the authors.
This implicit normalisation turns singular for 
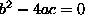and,
following the observations in [7], we can say that the
minimisation tends to ``pull'' the solution away from singularities;
in our case the singularity is a parabola and so the unique elliptical
solution tends to be biased towards low eccentricity, which explains
many of the following results, such as those in Figure 
.
