Now we want to generalize the definition and the computation of the Fourier transform from the regular sampling to the irregular sampling domain. In the general case, the definition of the Nonuniform Discrete Fourier Transform (NDFT) is the same as the one given by Equation 3, taking into consideration that the samples can the taken at irregular intervals both in time (
) and/or in frequency (
).
However, in practice, we want to take into consideration a more restricted case, which is the case where the samples are irregularly taken in the time domain t but regularly taken in the frequency domain. That is to say that the samples P(m) of the irregular Fourier transform are taken at multiples of a quantity 
, which is a fixed quantity in the Fourier domain. The fixed quantity in the regular case corresponds to 
. The extension from regular to irregular sampling, therefore, depends on the duration of the signal p(t) and not on the fact that the samples are taken at regular or irregular intervals.
The definition of the nonuniform discrete Fourier transform (NDFT) is as follows:
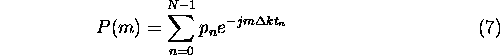
It is common practice to set 
where T is the range of extension for the samples . In that case the formulation of the NDFT is very similar to the one of the DFT except of the presence of the spatial coordinates instead of the index n. In this case, the NDFT is defined as:
From a computational point of view, two differences have to be noticed between DFT and NDFT.
The first difference is that samples in frequency are taken at intervals in the irregular case instead of 
in the regular case (T being the duration of the signal p(t), with 
, and N is the number of samples of the signal p(t)). The second difference is that, instead of the integer index n in the regular case, in the irregular case the irregular sampling coordinate appears in the exponent.