Binford has presented a report on the status of research in computer-based vision and image understanding currently under way at the Stanford Robotics Laboratory [8]. In particular, he focuses on a system he has developed called SUCCESSOR, which is designed to interpret images from multiple input sensors (including stereo images) and perform segmentation, enhancement, object identification, and visualization. I will focus more on his efforts in model-based image segmentation in this review.
Binford proposed a dual hierarchical image understanding technique in
which image values, structures, and shape descriptors are combined to
form hypotheses about objects to be recognized [7]. At
each level of this hierarchical process, information from the image is
matched against a prediction model (see
Figure ![]() for a conceptual diagram that
illustrates this approach).
for a conceptual diagram that
illustrates this approach).
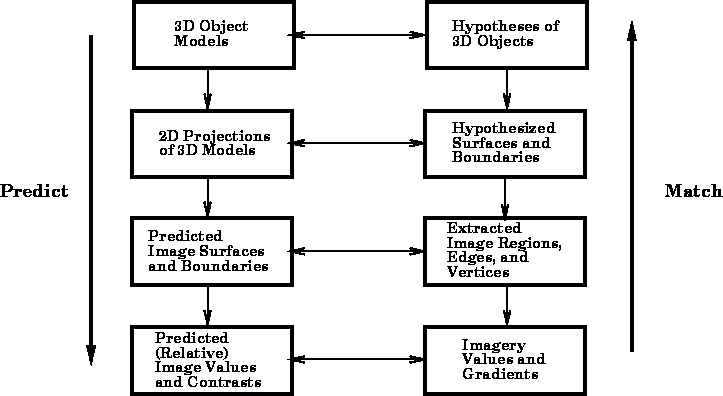
Figure: The conceptual diagram of the hierarchical image
interpretation model developed by Binford.
Starting from the top left side of the diagram, the process is driven by a three-dimensional model of the objects to be detected and their geometric relationships to one another. Using an estimated viewing perspective of the imaging device, the first step is to predict which objects are most likely to be visible, and project those objects onto the imaging planes based on the known geometric characteristics of the image sensors. The knowledge of the imaging modality is then used to predict the contrasts in the image based the material properties of the objects. The predicted contrasts are used to match the predicted edges, boundaries, regions, and textures against those found in the actual images using various low-level operators. When a reasonable (but possibly incomplete) match is found at the lowest level, the process can proceed to extract and match higher-level features (shown on the right side of the diagram). The regions, edges, and vertices extracted from the image operators can now be reliably combined into surfaces and boundaries that can then be combined into the three-dimensional objects to be detected. The advantage of the dual hierarchical approach is that it reduces the search space of hypotheses regarding how low-level image features are combined into higher-level abstractions. The prediction hierarchy (left side) prunes the search space so that the extraction hierarchy (right side) can perform more refined image processing operations. As a result, Binford's technique potentially can provide more accurate image interpretations than would be possible using a single-sided extraction hierarchy.
One of the basic principles behind Binford's approach to segmentation is to utilize as much information as possible about the geometries of the objects being modeled and the spatial relationships among these objects. Using this information, objects can be recognized more accurately from a wide variety of input sources. Furthermore, he claims that this recognition technique is more robust in the presence of noise and other ambiguities than existing algorithms that rely solely upon imaging properties. An added benefit of his model-based segmentation approach is that it can incorporate knowledge about the viewing parameters of the images and relate that knowledge to the geometric representations of the objects. This enables his system to utilize a rich set of models for understanding images and recognizing the objects contained within. These models have successfully been used to segment medical images, aerial photographs, indoor scenes for mobile robots, and recognition of industrial parts.
Binford also proposed models based on computational solid geometry
(CSG) techniques and representations of straight homogeneous
generalized cylinders (SHGC) and curved surfaces of revolution (CSR).
These models can represent a wide variety of objects and are
especially suited for objects that exhibit some degree of symmetry
(e.g., spinal segments and disks). Once a primary object axis has
been identified, this modeling technique can represent a wide variety
of topologies by sweeping out specific functions of the form
f(r,theta) along a straight, three-dimensional path, or by sweeping a
constant function along a curved three-dimensional path (see
Figure ![]() ). These geometrical representations can be
combined with basic set operations (such as intersection and union) to
construct more complicated composite objects. Directed acyclical
graphs (DAGs) are used to represent hierarchical relationships among
the various subobjects that form these composite objects. This
representation has also been extended to incorporate Bayesian models
of uncertainty to perform evidential reasoning under uncertainty.
). These geometrical representations can be
combined with basic set operations (such as intersection and union) to
construct more complicated composite objects. Directed acyclical
graphs (DAGs) are used to represent hierarchical relationships among
the various subobjects that form these composite objects. This
representation has also been extended to incorporate Bayesian models
of uncertainty to perform evidential reasoning under uncertainty.
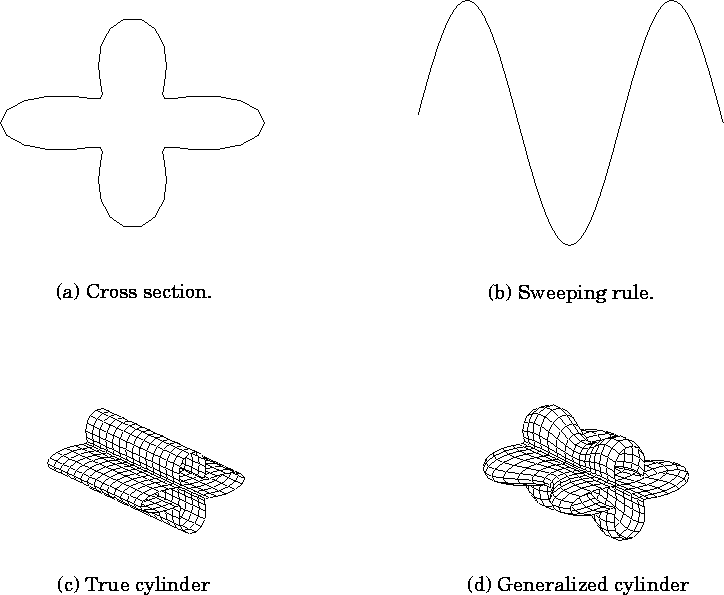
Figure: A straight homogeneous generalized cylinder
(SHGC) is defined by two functions. The first function defines
the cross-section (a) of the cylinder. The second function is
the sweeping rule (b), which modulates the width of the cylinder
(c) through the transverse axis to create the final SHGC (d).
In the SUCCESSOR system, once the objects to be modeled have been parameterized and represented using DAGs, image segmentation can be viewed as a process for fitting the contours of the modeled object to data points in the image. Several approaches can be used to perform the fitting. In one approach, an implicit equation can be derived to directly fit the predicted contour with the observed data. Another approach is to construct a wire-frame model of the composite object, apply an error bound to the frame, and direct the search for contours in the image data. The wire-frame model can be adjusted to account for object-to-object variation as well as variations in the viewing parameters (e.g., position, scale, and orientation). Regrettably though, Binford provides no quantitative results of any of the image understanding projects. Instead, he refers interested readers to more detailed papers written by various graduate students in the lab.