Definitions

A polygon $P$ is rectilinear if its interior angles belong to $\left\{\frac{\pi}{2}, \frac{3\cdot \pi}{2}\right\}$.

The Euclidean length of the straight line segment $e = [(x_{1}, y_{1}), (x_{2}, y_{2})]$ is $l_2 (e) = \sqrt{(x_1 - x_2)^2+(y_1-y_2)^2}$, while the length of $e$ according to the $l_1$ metric is $l_1(e) = \vert x_1-x_2\vert+\vert y_1-y_2\vert$.

${\cal P}_2(P)$ will denote the Euclidean perimeter of $P$, while ${\cal P}_1(P)$ will denote the perimeter of $P$ in the sense of $l_1$ metrics.

Since isometric polygons do not necessarily have the same perimeter under the $l_1$ metric, we shall use ${\cal P}_1(P, \alpha)$ for the $l_1$ perimeter of the polygon which is obtained by the rotating $P$ by the angle $\alpha$ with the origin as the centre of rotation.

Figure: For the given rectilinear $20$-gon $P$, its $l_1$ perimeter ${\cal P}_1(P)$ has the minimum value if the coordinate axes are chosen to be parallel with $u$ and $v$, while it reaches its maximum if the coordinate axes are parallel to $p$ and $q$.

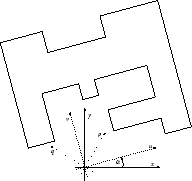Theorem 1. A given polygon $P$ is rectilinear if and only if there exists a choice of the coordinate system such that the Euclidean perimeter of $P$ and the $l_1$ perimeter of $P$ coincide, i.e.,

$${\cal P}_2 (P) \; = \; {\cal P}_1 (P, \alpha)\qquad \makebox{for some} \quad \alpha \; .$$