

Next:ImplementationUp:Kernel
Principal Component AnalysisPrevious:Kernel
Principal Component Analysis
Introduction
Kernel Principal Component Analysis (Kernel PCA) [5,6]
is a method of non-linear feature extraction, closely related to methods
applied in Support Vector Machines (SVMs)[3].
Suppose we have an input data set 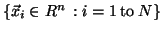 ,
where the distribution of the data is non-linear. One way to deal
with such a distribution is to attempt to linearise it by non-linearly
mapping the data from the input space
,
where the distribution of the data is non-linear. One way to deal
with such a distribution is to attempt to linearise it by non-linearly
mapping the data from the input space 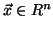 to a new feature space,
to a new feature space, 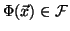 .
Kernel PCA and SVMs both use such a mapping. The mapping
.
Kernel PCA and SVMs both use such a mapping. The mapping 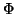 is defined implicitly, by specifying the form of the dot product in the
feature space. So, for an arbitrary pair of mapped data points, the dot
product is defined in terms of some kernel function thus:
is defined implicitly, by specifying the form of the dot product in the
feature space. So, for an arbitrary pair of mapped data points, the dot
product is defined in terms of some kernel function thus:
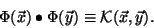
Some commonly used kernels are:
-
Gaussian:
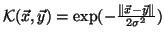
-
Dot Product Kernels, for example:
-
Sigmoid:
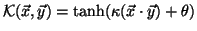
-
Polynomial:
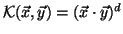
The key point to note is that any algorithm which can be expressed solely
in terms of dot products can then be implemented in the Feature Space  .
Applying a hyperplane classifier or linear function fitting leads to the
usual SVM classifiers and SVM Regression respectively. Applying linear
PCA in the feature space leads to Kernel PCA in the input space.
.
Applying a hyperplane classifier or linear function fitting leads to the
usual SVM classifiers and SVM Regression respectively. Applying linear
PCA in the feature space leads to Kernel PCA in the input space.


Next:ImplementationUp:Kernel
Principal Component AnalysisPrevious:Kernel
Principal Component Analysis
Carole Twining
2001-10-02