


Next: Metric constraints and
Up: Factorization under perspective
Previous: Depth estimation using
Although the above-mentioned depth recovery algorithm is non-iterative,
the final accuracy of reconstruction highly depends on the accurate
estimation of the fundamental matrices. Moreover, it does not embody one
of the nice feature of the affine factorization method, that is, use of
all of the images at the same time in a uniform manner. This problem can
be resolved by estimating depths in an iterative
manner[1,5,15].
Let 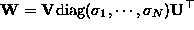 be SVD of the measurement matrix
be SVD of the measurement matrix  with singular values
with singular values
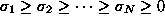 . If there is
no noise in
. If there is
no noise in 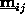 ,
, 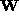 is rank 4 and hence
is rank 4 and hence 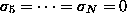 . With the presence of noise,
. With the presence of noise, 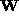 is
not exactly rank 4. If the noise is small, however,
is
not exactly rank 4. If the noise is small, however, 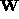 is
still nearly rank 4 and
is
still nearly rank 4 and 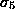 through
through 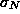 are almost zero.
So, we define a measure indicating the rank 4 proximity of
are almost zero.
So, we define a measure indicating the rank 4 proximity of 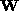 as
as

and estimate depths {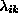 } which minimize this measure as a
criterion.
} which minimize this measure as a
criterion.
Let 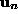 and
and 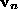 be n-th column of
be n-th column of
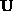 and
and 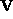 respectively. Differentiating
both sides of
respectively. Differentiating
both sides of 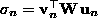 and
using relations
and
using relations 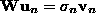 ,
,
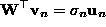 and
and
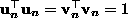 , we obtain
, we obtain
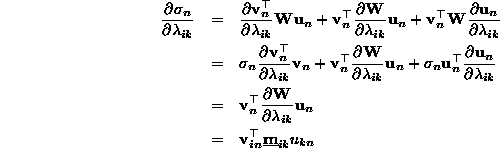
with 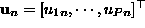 and
and
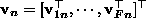 , where each
, where each
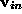 is a 3-vector corresponding to i-th frame. Using this
equation, we can compute first derivatives of J with respect to
is a 3-vector corresponding to i-th frame. Using this
equation, we can compute first derivatives of J with respect to
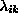 . Therefore J can be minimized by standard optimization
technique such as a conjugate gradient method. Computing second
derivatives is also possible which allows to adopt Newton-like methods.
We initialize the minimization process by taking
. Therefore J can be minimized by standard optimization
technique such as a conjugate gradient method. Computing second
derivatives is also possible which allows to adopt Newton-like methods.
We initialize the minimization process by taking 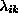 as unity
for all i and k which means we start with an affine projection.
F+P-1 depth parameters are fixed throughout the iteration process as
stated in (12).
as unity
for all i and k which means we start with an affine projection.
F+P-1 depth parameters are fixed throughout the iteration process as
stated in (12).
Bob Fisher
Wed Apr 21 20:23:11 BST 1999
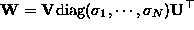 be SVD of the measurement matrix
be SVD of the measurement matrix 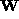 with singular values
with singular values
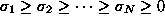 . If there is
no noise in
. If there is
no noise in 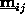 ,
, 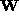 is rank 4 and hence
is rank 4 and hence 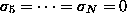 . With the presence of noise,
. With the presence of noise, 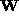 is
not exactly rank 4. If the noise is small, however,
is
not exactly rank 4. If the noise is small, however, 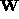 is
still nearly rank 4 and
is
still nearly rank 4 and 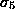 through
through 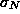 are almost zero.
So, we define a measure indicating the rank 4 proximity of
are almost zero.
So, we define a measure indicating the rank 4 proximity of 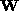 as
as




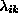 } which minimize this measure as a
criterion.
} which minimize this measure as a
criterion.
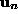 and
and 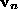 be n-th column of
be n-th column of
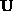 and
and 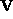 respectively. Differentiating
both sides of
respectively. Differentiating
both sides of 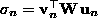 and
using relations
and
using relations 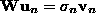 ,
,
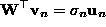 and
and
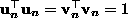 , we obtain
, we obtain
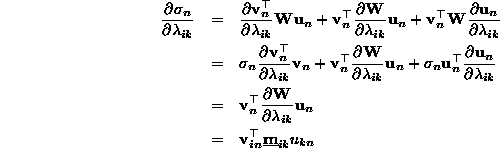
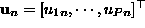 and
and
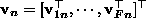 , where each
, where each
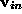 is a 3-vector corresponding to i-th frame. Using this
equation, we can compute first derivatives of J with respect to
is a 3-vector corresponding to i-th frame. Using this
equation, we can compute first derivatives of J with respect to
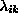 . Therefore J can be minimized by standard optimization
technique such as a conjugate gradient method. Computing second
derivatives is also possible which allows to adopt Newton-like methods.
We initialize the minimization process by taking
. Therefore J can be minimized by standard optimization
technique such as a conjugate gradient method. Computing second
derivatives is also possible which allows to adopt Newton-like methods.
We initialize the minimization process by taking 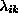 as unity
for all i and k which means we start with an affine projection.
F+P-1 depth parameters are fixed throughout the iteration process as
stated in (
as unity
for all i and k which means we start with an affine projection.
F+P-1 depth parameters are fixed throughout the iteration process as
stated in (