


Next: Recognition phase
Up: published in proceedings Forth
Previous: Four-dimensional geometric feature
The four-dimensional feature distribution as sampled from a surface in 3D
space is described by a histogram.
Each feature 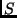 is mapped onto exactly one bin
is mapped onto exactly one bin 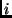 of the histogram
of the histogram
 ,
,
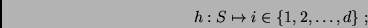 |
(9) |
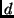 is the number of bins in the histogram.
The mapping
is the number of bins in the histogram.
The mapping 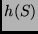 is defined by quantizing each of the four feature dimensions
in five equal intervals.
The resulting number of
is defined by quantizing each of the four feature dimensions
in five equal intervals.
The resulting number of 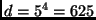 bins for the complete histogram is both
easy to handle and sufficient for classification.
The length dimension
bins for the complete histogram is both
easy to handle and sufficient for classification.
The length dimension  [cf. Equation (8)] is normalized to the
maximal occurring length
[cf. Equation (8)] is normalized to the
maximal occurring length  .
An entry
.
An entry  of the histogram is the normalized frequency of features
of the histogram is the normalized frequency of features  that are mapped onto bin
that are mapped onto bin 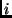 ,
,
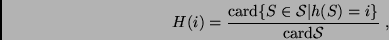 |
(10) |
where 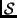 is the set of all sampled features and
card denotes the cardinality of a set.
is the set of all sampled features and
card denotes the cardinality of a set.
When working with meshed surfaces, it is a good idea to collect for training
all samples from multiple meshes of the same surface.
In this way, we incorporate variations introduced by the mesh procedure.
The histogram  together with the maximal length
together with the maximal length  constitute an
object model.
The additional information of
constitute an
object model.
The additional information of  is necessary for scaling at
recognition time.
We store a collection of such models in a database, one for each object we want
to recognize.
is necessary for scaling at
recognition time.
We store a collection of such models in a database, one for each object we want
to recognize.



Next: Recognition phase
Up: published in proceedings Forth
Previous: Four-dimensional geometric feature
Eric Wahl
2003-11-06
![]() together with the maximal length
together with the maximal length ![]() constitute an
object model.
The additional information of
constitute an
object model.
The additional information of ![]() is necessary for scaling at
recognition time.
We store a collection of such models in a database, one for each object we want
to recognize.
is necessary for scaling at
recognition time.
We store a collection of such models in a database, one for each object we want
to recognize.