

Next: High Resolution Tracking of
Up: Harmonic Maps
Previous: Harmonic Maps
Introduction
A harmonic map
 can be viewed as an embedding
from a manifold
can be viewed as an embedding
from a manifold 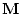 with disk topology to a planar domain
with disk topology to a planar domain
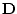 . A harmonic map is a critical point for the harmonic
energy functional,
. A harmonic map is a critical point for the harmonic
energy functional,
and can be calculated by minimizing 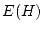 . The norm of the
differential
. The norm of the
differential 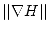 is given by the metric on
is given by the metric on 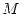 and
and 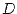 ,
and
,
and 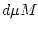 is the measure on
is the measure on 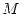 [7,5,1,2].
Since our source manifold
[7,5,1,2].
Since our source manifold 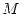 is in the form of a discrete
triangular mesh, we approximate the harmonic energy as
[1,11,3],
is in the form of a discrete
triangular mesh, we approximate the harmonic energy as
[1,11,3],
![\begin{displaymath}
E(H)=\sum_{[v_0,v_1]} k_{[v_0,v_1]} \vert\vert H(v_0)-H(v_1)\vert\vert^2,
\end{displaymath}](img15.png) |
(1) |
where ![$[v_0,v_1]$](img16.png) is an edge connecting two neighboring vertices
is an edge connecting two neighboring vertices
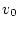 and
and 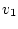 , and
, and ![$k_{[v_0,v_1]}$](img19.png) is defined as
is defined as
where
 and
and
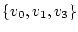 are two conjoined
triangular faces.
are two conjoined
triangular faces.
By minimizing the harmonic energy, a harmonic map can be computed
using the Euler-Lagrange differential equation for the energy
functional, i.e.
 |
(2) |
where 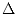 is the Laplace-Beltrami operator
[7,5,1,2].
This will lead to solving a sparse linear least-square system for
the mapping
is the Laplace-Beltrami operator
[7,5,1,2].
This will lead to solving a sparse linear least-square system for
the mapping 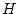 of each vertex
of each vertex 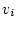 [1,11,3]. If the boundary
condition is given,
[1,11,3]. If the boundary
condition is given,
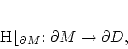 |
(3) |
then the solution exists and is unique.
The theory of harmonic maps is based on conformal geometry theory
[3,8]; the harmonic map between two
topological disks is a diffeomorphism with minimal stretching energy
and bounded angle distortion. Harmonic maps are invariant for the
same source surface with different poses, thus making it possible to
account for global rigid motion. Harmonic maps are highly
continuous, stable and robust to noise. They depend on the geometry
in a continuous manner.
Harmonic maps have many merits which are valuable for computer
vision applications:
- First, the harmonic map is computed through global
optimization, and takes into account the overall surface topology.
Thus it does not suffer from local minima, folding,
clustering, which are common problems due to local optimization.
- Second, the harmonic map is not sensitive to the
resolution of the surface, and to the noise on the surface. Even if
the data for the input surface is noisy, the result won't be
affected significantly.
- Third, the harmonic map doesn't require the surface to
be smooth. It can be accurately computed even when the surface
includes sharp features.
- Forth, since the range of the map of an open surface is a unit disk
which is convex, the harmonic map exists, and is a
diffeomorphism, namely, the map is one to one and on-to. So
it can allow us to establish correspondences on 2D and recover 3D
registration from the same mapping.
- Fifth, the harmonic map is determined by the metric, not
the embedding. This implies that the harmonic map is invariant
for the same surface with different poses. Furthermore, if there is
not too much stretching between two surfaces undergoing non-rigid
deformations, they will induce similar harmonic maps.
Furthermore, harmonic maps are easy to compute and robust to
numerical errors. By using a traditional finite element method
[4], they are easy to implement.


Next: High Resolution Tracking of
Up: Harmonic Maps
Previous: Harmonic Maps
Yang Wang
2006-02-15
![]() can be viewed as an embedding
from a manifold
can be viewed as an embedding
from a manifold ![]() with disk topology to a planar domain
with disk topology to a planar domain
![]() . A harmonic map is a critical point for the harmonic
energy functional,
. A harmonic map is a critical point for the harmonic
energy functional,