

Next: Characteristic Views
Up: Increased Extent of Characteristic
Previous: Introduction
Shape from Shading
Shape-from-shading (SFS) has been an active subject of research for over two decades, and may be regarded as one of the classical problems of computer vision.
In recent research we have developed a SFS technique based upon the variational approach of Horn and Brooks [20,21,22]. Our scheme addresses one of the main problems with the Horn and Brooks technique - its tendency to over-smooth the recovered needle-map, leading to a loss of detail in regions where the surface orientation varies rapidly. Several other solutions have been proposed to this (e.g. [23]), but our research has shown that the apparatus of robust statistics may be applied to the problem with encouraging results [17,18].
In brief, we wish to solve the normalized image irradiance equation
where E(x,y) is the image of the object, and R(p,q) is the reflectance of a surface patch oriented such that its normal has direction
n=(-p,-q,1)T. The quantities p and q are
the
components
of the surface gradient in the x and y direction respectively, i.e.
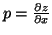 and
and
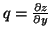 .
.
If the surface is assumed to have Lambertian reflectance properties, the brightness of a patch will simply be proportional to the angle between the surface normal and the light source direction,
s. The image irradiance equation then becomes
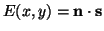 .
Unfortunately, this is under-constrained for the recovery of p and q over most of an object's surface. Hence, we must introduce an additional constraint on the smoothness of the recovered needle-map. This is encoded by
constructing an energy functional of the form
.
Unfortunately, this is under-constrained for the recovery of p and q over most of an object's surface. Hence, we must introduce an additional constraint on the smoothness of the recovered needle-map. This is encoded by
constructing an energy functional of the form
where
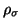 may be any regularization function, and
may be any regularization function, and 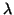 is a Lagrange multiplier. The first term of this functional encodes the image irradiance equation. The second term uses the derivatives of the recovered normals to penalize sharp changes of orientation according to the function
is a Lagrange multiplier. The first term of this functional encodes the image irradiance equation. The second term uses the derivatives of the recovered normals to penalize sharp changes of orientation according to the function
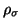 .
.
Applying the calculus of variations and discretizing the resulting Euler equation, we develop the following generalized update equation for iteratively estimating the surface normals
In the quadratic case where
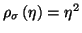 ,
this becomes the update equation used by Horn and Brooks [20]. However, any other function may be used as the regularization term, and we have investigated several robust measures, including the classical Tukey [24] and Huber [25], and the Adaptive Prior Potential Functions of Li [26]. We also introduced [18] a continuous version of the piecewise Huber robust estimator, described by
,
this becomes the update equation used by Horn and Brooks [20]. However, any other function may be used as the regularization term, and we have investigated several robust measures, including the classical Tukey [24] and Huber [25], and the Adaptive Prior Potential Functions of Li [26]. We also introduced [18] a continuous version of the piecewise Huber robust estimator, described by
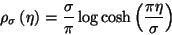 |
(2) |
and found that this yielded the best results by offering a compromise between over-smoothing and noise rejection/numerical stability.


Next: Characteristic Views
Up: Increased Extent of Characteristic
Previous: Introduction
Philip Worthington
1998-10-28
![]() .
Unfortunately, this is under-constrained for the recovery of p and q over most of an object's surface. Hence, we must introduce an additional constraint on the smoothness of the recovered needle-map. This is encoded by
constructing an energy functional of the form
.
Unfortunately, this is under-constrained for the recovery of p and q over most of an object's surface. Hence, we must introduce an additional constraint on the smoothness of the recovered needle-map. This is encoded by
constructing an energy functional of the form
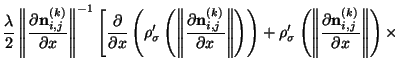
![$\displaystyle \left({\mathbf n}_{i+1,j}^{(k)} + {\mathbf n}_{i-1,j}^{(k)} - \le...
...l x^2}\right){{\partial {\mathbf n}_{i,j}^{(k)}}\over{\partial x}}\right)\Bigg]$](img13.gif)
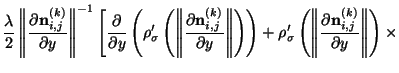
![$\displaystyle \left({\mathbf n}_{i,j+1}^{(k)} + {\mathbf n}_{i,j-1}^{(k)} - \le...
...l y^2}\right){{\partial {\mathbf n}_{i,j}^{(k)}}\over{\partial y}}\right)\Bigg]$](img15.gif)
![]() ,
this becomes the update equation used by Horn and Brooks [20]. However, any other function may be used as the regularization term, and we have investigated several robust measures, including the classical Tukey [24] and Huber [25], and the Adaptive Prior Potential Functions of Li [26]. We also introduced [18] a continuous version of the piecewise Huber robust estimator, described by
,
this becomes the update equation used by Horn and Brooks [20]. However, any other function may be used as the regularization term, and we have investigated several robust measures, including the classical Tukey [24] and Huber [25], and the Adaptive Prior Potential Functions of Li [26]. We also introduced [18] a continuous version of the piecewise Huber robust estimator, described by